- Negative index metamaterials
-
Negative index metamaterials or negative index materials (NIM) are artificial structures where the refractive index has a negative value over some frequency range.[1] This does not occur in any known natural materials, and thus is only achievable with engineered structures known as metamaterials. Metamaterial refers broadly to any synthetic material with unusual refractive properties, among other descriptions.
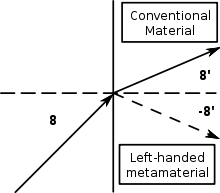
Metamaterials which exhibit a negative value for the refractive index (NIM) are often referred to by any of several names and terminologies: "left-handed media (LHM), backward wave media (BW media), media with negative refractive index, double negative (DNG) metamaterials, and other similar names.[2]
Properties and characteristics
Metamaterials are incarnations of materials first proposed by a Russian theorist Victor Veselago in 1967.[3] The proposed left-handed or negative index materials were theorized to exhibit optical properties opposite to those of glass, air, and the other transparent media. Such materials were predicted to exhibit counter intuitive properties, like bending, or refracting, light in unusual and unnatural ways. The first metamaterial was constructed 33 years later.[1][2][3][4]
Such negative index metamaterials are being developed in order to manipulate electromagnetic radiation in new ways. For example, optical and electromagnetic properties of natural materials are often altered through chemistry. With metamaterials optical and electromagnetic properties can be engineered through the geometry of its unit cells. The unit cells are materials that are ordered in geometric arrangements with dimensions that are fractions of the wavelength of the radiated electromagnetic wave. Each artificial unit responds to the radiation from the source. The collective result is a material's response to the electromagnetic wave that is broader than normal.[1][2][4]
By having the freedom to alter effects by adjusting the configurations and sizes of the unit cells, control over material parameters known as permittivity and magnetic permeability can be achieved. These two parameters (or quantities) determine the propagation of electromagnetic waves in matter. In other words, the achievable electromagnetic and optical effects can be extended. For example by controlling the values of permittivity and permeability the refractive index can be negative, or zero. Optical properties can be expanded beyond the capabilities of lenses, mirrors, and other conventional materials. One of the effects most studied is the negative index of refraction.[1][2][3][4]
When a negative index of refraction occurs propagation of the electromagnetic wave is reversed. Resolution below the diffraction limit becomes possible. This is known asSubwavelength imaging. Transmitting a beam of light via an electromagnetically flat surface is another capability. In contrast, conventional materials are usually curved, and cannot achieve resolution below the diffraction limit. Also, reversing the electromagnetic waves in a material, in conjunction with other ordinary materials (including air) could result in minimizing losses that would normally occur.[1][2][3][4]
The reverse of the electromagnetic wave, characterized by an antiparallel phase velocity is also an indicator of negative index of refraction.[1][3]
Furthermore, negative index materials are customized composites. In other words, combinations of materials designed to achieve optical properties not seen in nature. The properties stem from the unique lattice structure of the composite material, with features smaller than the wavelength of interest separated by distances that are also smaller than the wavelength of interest. By fabricating such metamaterials, researchers are trying to overcome fundamental limits tied to the wavelength of light.[1][2][4]
The electromagnetic wave hitting a metamaterial is transformed into electromagnetic waves of a different variety, which are shorter in wavelength than the incident radiation. This transformation leads to unusual and counter intuitive properties that might be harnessed for practical use.[4][5]
Materials
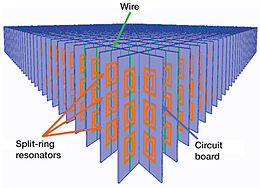
The first actual metamaterials worked in the microwave regime, or centimeter wavelengths, of the electromagnetic spectrum (about 4.3 GHz). It was constructed of split-ring resonators and conducting straight wires (as unit cells). The unit cells were sized from 7 to 10 millimeters.
The unit cells were arranged in a two-dimensional (periodic) repeating pattern; a crystal-like geometry. Both, the unit cells and the lattice spacing were smaller than the radiated electromagnetic wave. This produced the first left-handed material when both the permittivity and permeability of the material were negative.
Research in the microwave range continued with split-ring resonators and conducting wires. Research also continued in the shorter wavelengths with this configuration of materials with scaled down unit cell sizes. However, at around 200 THz issues arise which make using the split ring resonator problematic. "Alternative materials become more suitable for the THz and optical regimes". At these wavelengths selection of materials and size limiations become important.[1][6][7][8]
The challenge is to fabricate metamaterials so that they refract light at ever-smaller wavelengths.[9]
Applications
Negative index metamaterials show potential to be employed in various electromagnetic components and devices. Metamaterial antennas are commercially available in the wireless domain, and these metamaterial apparatuses continue to be researched. Other potential applications are for microwave radar absorbers, electrically small resonators, waveguides that can go beyond the diffraction limit, phase compensators, advancements in focusing devices (e.g. microwave lens), and improved electrically small antennas.[10][11][12][13]
In the optical frequency regime developing the superlens may allow for imaging below the diffraction limit. Other potential applications for negative index metamaterials are optical nanolithography, nanotechnology circuitry, A near field superlens (Pendry, 2000) could be useful for biomedical imaging and subwavelength photolithography.[13]
Implications of negative refractive materials
The existence of negative refractive materials can result in a change in electrodynamic calucalations for the case of permeability μ = 1 . A change from a conventional refractive index to a negative value gives incorrect results for conventional calculations, because some properties and effects have been altered. When permeability μ has values other than 1 this affects Snell's law, the Doppler effect, the Cherenkov radiation, Fresnel's equations, and Fermat's principle.[8]
The refractive index is basic to the science of optics. Shifting the refractive index to a negative value may be a cause to revisit or reconsider the interpretation of some norms, or basic laws.[13]
Manipulating permittivity and permeability
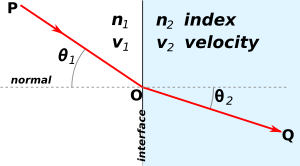 Refraction of light at the interface between two media of different refractive indices, with n2 > n1. Since the velocity is lower in the second medium (v2 < v1), the angle of refraction θ2 is less than the angle of incidence θ1; that is, the ray in the higher-index medium is closer to the normal.
Refraction of light at the interface between two media of different refractive indices, with n2 > n1. Since the velocity is lower in the second medium (v2 < v1), the angle of refraction θ2 is less than the angle of incidence θ1; that is, the ray in the higher-index medium is closer to the normal.
To describe any electromagnetic properties of a given material such as an optical lens, two significant parameters should be noted. These are permittivity, ε, and permeability, μ, which could allow for accurate prediction of light waves traveling of within materials, and electromagnetic phenomena that occur at the surface between two materials (interface).[14]
For example, refractive index is an electromagnetic phenomenon which occurs at the surface (or interface) between two materials. Snell's law states that the relationship between the radiated angle of incidence, and the resulting refracted angle of transmission, rests on the refractive index, n, of the two media (materials). Mathematics provides a visualization with
 . Hence, it can be seen that the behavior of the refractive index is dependent on the association of these two parameters, as well as their quantitative values. Therefore, if designed or arbitrarily modified values can be inputs for ε, and, μ then the behavior of propagating electromagnetic waves inside the material can be manipulated at will. This ability then allows for intentional determination of the refractive index.[14]Video representing negative refraction of light at uniform planar interface.
. Hence, it can be seen that the behavior of the refractive index is dependent on the association of these two parameters, as well as their quantitative values. Therefore, if designed or arbitrarily modified values can be inputs for ε, and, μ then the behavior of propagating electromagnetic waves inside the material can be manipulated at will. This ability then allows for intentional determination of the refractive index.[14]Video representing negative refraction of light at uniform planar interface.
For example, in 1967, Victor Veselago analytically determined that light will refract in the reverse direction (negatively) at the interface between a material with negative refractive index and a material exhibiting conventional refractive index. This extraordinary material was realized, on paper, with simultaneous negative values for ε, and, μ, and could be termed a double negative material. However, in Veselago's day, a material which exhibits double negative parameters simultaneously seemed impossible, because no natural materials exist which can produce this effect. Therefore his work was ignored for three decades.[14]
In general, the physical properties of natural materials cause limitations. Most dielectrics only have positive permittivities, ε > 0 . Metals will exhibit negative permittivity, ε < 0 at optical frequencies, and plasmas exhibit negative permittivity values in certain frequency bands. Pendry et al. demonstrated that the plasma frequency can be made to occur in the lower microwave frequencies for metals, with an effective medium of metal rods that replaces the bulk metal. However, in each of these cases permeability remains always positive. At microwave frequencies, it is possible for negative μ to occur in some ferromagnetic materials. But, the inherent drawback is they are difficult to find above terahertz frequencies. In any case, a natural material that can achieve negative values for permittivity and permeability simultaneously has not been found, or discovered. Hence, all of this has led to constructing artificial composite materials known as metamaterials to achieve desired results.[14]
Physical properties never before produced in nature
Theoretical articles were published in 1996 and 1999 which showed that synthetic materials could be constructed to purposely exhibit an negative permittivity and permeability.[note 1]
These papers, along with Veselago's 1967 theoretical analysis of the properties of negative index materials, provided the background to fabricate a metamaterial with negative effective permittivity and permeability.[15][16][17] (See below)
A metamaterial developed to exhibit negative index behavior is typically formed from individual components. Each component responds independently and differently to a radiated electromagnetic wave as it travels through the material. Since these components are smaller than the radiated wavelength it is understood that a macroscopic view includes an effective value for both permittivity and permeability.[15]
Composite material
 A split-ring resonator array arranged to produce a negative index of refraction, constructed of copper split-ring resonators and wires mounted on interlocking sheets of fiberglass circuit board.
A split-ring resonator array arranged to produce a negative index of refraction, constructed of copper split-ring resonators and wires mounted on interlocking sheets of fiberglass circuit board.
The total array consists of 3 by 20×20 unit cells with overall dimensions of 10×100×100 milimeters.[6][18] The height of 10 milimeters measures a little more than six subdivision marks on the ruler, which is marked in inches.
Credit: NASA Glenn Research Center.In the year 2000 a team of UCSD researchers produced a new class of composite materials which exhibited unusual physical properties that were never before produced in nature. These materials obey the laws of physics, but behave differently from normal materials. In essence these negative index metamaterials were noted for having the ability to reverse many of the physical properties that govern the behavior of ordinary optical materials. One of those unusual properties is the ability to reverse, for the first time, Snell's law of refraction. Until the demonstration by the UCSD team, the material was unavailable. Advances during the 1990s in fabrication and computation abilities allowed these first metamaterials to be constructed. Thus, the "new" metamaterial was tested for the effects described by Victor Veselago 30 years earlier, but only at first in the microwave frequency domain. Reversal of phase velocity was established during this first test. Studies of this experiment, which followed shortly thereafter, announced that other effects had occurred.[15][16][18][19]
To date (March 2010) these materials have only been commonly demonstrated at wavelengths longer than those in the visible spectrum. In addition, NIMs are fabricated from opaque materials, and usually made of non-magnetic constituents. However, as an illustration – if these materials could be demonstrated at visible frequencies, and a flashlight is shone on a NIM slab, the material should focus the light at a point on the other side. This is not possible with a sheet of ordinary opaque material.[1][18][19]
When first demonstrated this composite material (NIM) was limited to transmitting microwave radiation at frequencies of 4 to 7 gigahertz. This is approximated to be the range of operating frequencies between household microwave ovens(2.45 GHz) and military radars (10 GHz). At demonstrated frequencies, pulses of electromagnetic radiation moving through the material in one direction are composed of constituent waves moving in the opposite direction.[18][19][20]
The metamaterial was constructed as a periodic array of copper conducting elements. The design was such that the cells, and the lattice spacing between the cells, were much smaller than the radiated electromagnetic wavelength. Hence, it behaves as an effective medium. The material has become notable because its range of (effective) permittivity εeff and permeability μeff values have exceeded those found in any ordinary material. Furthermore, the characteristic of negative (effective) permeability evinced by this medium is particularly notable, because it has not been found in ordinary materials. In addition, the negative values for the magnetic component is directly related to its left-handed nomenclature, and properties (discussed in a section below). The split-ring resonator (SRR), based on the prior 1999 theoretical article, is the tool employed to achieve negative permeability. This first composite metamaterial is then composed of split-ring resonators and electrical conducting posts.[18]
With antiferromagnets and certain types of insulating ferromagnets, effective negative magnetic permeability is achievable when polariton resonance exists. However, to achieve a negative index of refraction, permittivity with negative values must occur within the same frequency range. The artificially fabricated split-ring resonator is a design that accomplishes this, along with the promise of dampening high losses. With this first introduction of the metamaterial, it appears that the losses incurred were smaller than antiferromagnetic, or ferromagnetic materials.[18]
Simultaneous negative permittivity and permeability
Negative permittivity εeff < 0 had already been discovered and realized in metals for frequencies all the way up to the plasma frequency, before the first metamaterial. There are two requirements to achieve a negative value for refraction. First, is to fabricate a material which can produce negative permeability μeff < 0. Second, negative values for both permittivity and permeability must occur simultaneously over a common range of frequencies.[1][15]
Therefore, for the first metamaterial, the nuts and bolts are one split-ring resonator electromagnetically combined with one (electric) conducting post. These are designed to resonate at designated frequencies to achieve the desired values. Looking at the make-up of the split ring, the associated magnetic field pattern from the SRR is dipolar. This dipolar behavior is notable because this means it mimics nature's atom, but on a much larger scale, such as in this case at 2.5 millimeters. Atoms exist on the scale of picometers.
The splits in the rings create a dynamic where the SRR unit cell can be made resonant at radiated wavelengths much larger than the diameter of the rings. If the rings were closed, a half wavelength boundary would be electromagnetically imposed as a requirement for resonance.[18] The first ever metamaterial with simultaneous effective permittivity and permeability was fabricated in the United States of America.
The split in the second ring is oriented opposite the split in the first ring. It is there to generate a large capacitance, which occurs in the small gap. This capacitance substantially decreases the resonant frequency while concentrating the electric field. The individual SRR depicted on the right had a resonant frequency of 4.845 GHz, and the resonance curve, inset in the graph, is also shown. The radiative losses from absorption and reflection are noted to be small, because the unit dimensions are much smaller than the free space, radiated wavelength.[18]
When these units or cells, are combined into a periodic arrangement the magnetic coupling between the resonators is strengthened, and a strong magnetic coupling occurs. Properties unique in comparison to ordinary or conventional materials begin to emerge. For one thing, this periodic strong coupling creates a material which now has an effective magnetic permeability μeff in response to the radiated-incident magnetic field.[18]
Composite material passband
Graphing the general dispersion curve, a region of propagation occurs from zero up to a lower band edge, followed by a gap, and then an upper passband. The presence of a 400 MHz gap between 4.2 GHz and 4.6 GHz implies a band of frequencies where μeff < 0 occurs.
(Please see the image in the previous section)
Furthermore, when wires are added symmetrically between the split rings, a passband occurs within the previously forbidden band of the split ring dispersion curves. That this passband occurs within a previously forbidden region indicates that the negative ´εeff for this region has combined with the negative μeff to allow propagation. This fit with theoretical predictions. Mathematically, the dispersion relation leads to a band with negative group velocity everywhere, and a bandwidth that is independent of the plasma frequency, within the stated conditions.[18]
Mathematical modeling and experiment have both shown that periodically arrayed conducting elements (non-magnetic by nature) respond predominately to the magnetic component of incident electromagnetic fields. The result is an effective medium and negative μeff over a band of frequencies. The permeability was verified to be the region of the forbidden band, where the gap in propagation occurred - from a finite section of material. This was combined with a negative permittivity material, εeff < 0, to form a “left-handed” medium, which formed a propagation band with negative group velocity where previously there was only attenuation. This validated predictions. In addition, a later work determined that this first metamaterial had a range of frequencies over which the refractive index was predicted to be negative for one direction of propagation (see ref #[1]). Other predicted electrodynamic effects were to be investigated in other research.[18]
Describing a left-handed material
From the conclusions in the above section a left-handed material (LHM) can be defined. It is a material which exhibits simultaneous negative values for permittivity, ε, and permeability, μ, in an overlapping frequency region. Since the values are derived from the effects of the composite medium system as a whole, these are defined as effective permittivity, εeff, and effective permeability, μeff. Real values are then derived to denote the value of negative index of refraction, and wave vectors. This means that in practice losses will occur for a given medium used to transmit electromagnetic radiation such as microwave, or infrared frequencies, or visible light - for example. In this instance, real values describe either the amplitude or the intensity of a transmitted wave relative to an incident wave, while ignoring the negligible loss values.[6][18]
Isotropic, negative index in two dimensions
In sections above, the first fabricated metamaterial was constructed with resonating elements, which exhibited one direction of incidence and polarization. In other words, this structure exhibited left-handed propagation in one dimension. This was discussed in relation to Veselago's seminal work 33 years earlier (1967). He predicted that intrinsic to a material which manifests negative values of effective permittivity and permeability, are several types of reversed physics phenomena. Hence, there was then a critical need for a higher dimensional LHMs to confirm Veselago's theory, as expected. The confirmation would include reversal of Snell's law (index of refraction), along with other reversed phenomena.
In the beginning of 2001 the existence of a higher dimensional structure was reported. It was two dimensional and demonstrated by both experiment and numerical confirmation. It was an LHM, a composite constructed of wire strips mounted behind the split-ring resonators (SRRs) in a periodic configuration. It was created for the express purpose of being suitable for further experiments to produce the Veselago predicted effects.[6]
Experimental verification of a negative index of refraction
According to Snell's law, when refraction of light is measured or observed for ordinary materials surrounded by air, the value is always greater than one, n > 1. A refracted ray entering a material from air will be bent towards, but never end up on the same side as the normal. In addition, the science and practice of optical lensing and imaging is based on the knowledge that any material with a refractive index different from its environment will alter the direction of incoming rays which do not arrive in a straight line in relation to the interface (of the material surface and air). Also, lenses have been designed to focus and steer the various spectra of light (EM radiation) in frequency ranges from radio to the visible spectra. Furthermore, all known natural occurring materials demonstrate refractive indices that are positive. However, a theoretical work in 1967 showed that a refractive index with negative values is possible and that this does not violate the laws of physics. As discussed previously (above), the first metamaterial had a range of frequencies over which the refractive index was predicted to be negative for one direction of propagation were reported in May of the year 2000.[1][22][23]
In 2001, a team of researchers constructed a prism composed of metamaterials (negative index metamaterials) to experimentally test for negative refractive index. The experiment used a waveguide to help transmit the proper frequency and isolate the material.[1][22][24][25][26][27][28]
The experimental demonstration of negative refractive index was followed by another demonstration, in 2003, of a reversal of Snell's law, or reversed refraction. However, in this experiment negative index of refraction material is in free space from 12.6 to 13.2 GHz. Although the radiated frequency range is about the same, a notable distinction is this experiment is conducted in free space rather employing waveguide.[29]
Furthering the authenticity of negative refraction, the power flow of a wave transmitted through a dispersive left-handed material was calculated and compared to a dispersive right-handed material. The transmission of an incident field, composed of many frequencies, from an isotropic nondispersive material into an isotropic dispersive media is employed. The direction of power flow for both nondispersive and dispersive media is determined by the time-averaged Poynting vector. Negative refraction was shown to be possible for multifrequency signals by explicit calculation of the Poynting vector in the LHM.[30]
Fundamental electromagnetic properties of the NIM
In a slab of conventional material, with an ordinary refractive index – a right-handed material (RHM) – the wave front is transmitted away from the source. In a NIM the wavefront travels toward the source. However, the magnitude and direction of the flow of energy essentially remains the same in both the ordinary material and the NIM. Since, the flow of energy remains the same in both materials (media) the impedance of the NIM matches the RHM. Hence, the sign of the intrinsic impedance is still positive in a NIM.[31][32]
Light incident on a left-handed material, or NIM, will bend to the same side as the incident beam, and for Snell’s law to hold, the refraction angle should be negative. In a passive metamaterial medium this determines a negative real and imaginary part of the refractive index.[2][31][32]
Negative refractive index in left-handed materials
In 1968 Victor Veselago's paper showed that the opposite directions of EM plane waves and the flow of energy was derived from the individual Maxwell curl equations. In ordinary optical materials, the curl equation for the electric field show a "right hand rule" for the directions of the electric field E, the magnetic induction B, and wave propagation, which goes in the direction of wave vector k. However, the direction of energy flow formed by E × H is right-handed only when permeability is greater than zero. This means that when permeability is less than zero, e.g. negative, wave propagation is reversed (determined by k), and contrary to the direction of energy flow. Furthermore, the relations of vectors E, H, and k form a "left-handed" system – and it was Veselago who coined the term "left-handed" (LH) material, which is in wide use today (2011). He contended that an LH material has a negative refractive index and relied on the steady-state solutions of Maxwell's equations as a center for his argument.[33]
After a 30 year void, when LH materials were finally demonstrated, it could be said that the designation of negative refractive index is unique to LH systems; even when compared to photonic crystals. Photonic crystals, like many other known systems, can exhibit unusual propagation behavior such as reversal of phase and group velocities. But, negative refraction does not occur in these systems, and not yet realistically in Photonic crystals.[33][34][35]
Negative refraction at visible frequencies
As of May 2010 - In previous years, several anomalous studies have announced negative refraction at one single frequency, or other, in the visible spectrum. But the results of two such demonstrations are considered ambiguous by later studies. Another most recent, published, demonstration at one single visible frequency is still not the norm, or common, for the large body of work that has been produced in the field of metamaterials. To date, hundreds of scientific, peer reviewed, articles have been published regading some aspect of metamaterials. This is compared to some minscule number, the studies that have apparent results in the visible spectrum. In an encyclopedia article such as this it is problematic to give undue weight to such studies, until these become common, or part of the norm, for metamaterials.[36]
Moreover, although previous research efforts have announced negative refraction of one single frequency in the visible light spectrum, this most recent (April, 2010) is being reported as "the first one that operates on visible light." Also as before, the stated achievement is for one single frequency in the visible spectrum. In other words there is no broad band ability.[37][38][39]
Experimental verification of reversed Cherenkov radiation
Besides reversed values for index of refraction, Veselago predicted the occurrence of reversed Cherenkov radiation (also known simply as CR) in a left-handed medium. In 1934 Pavel Cherenkov discovered a coherent radiation (laser) that occurs when certain types of media are bombarded by fast moving electron beams. In 1937 a theory built around CR stated that when charged particles, such as electrons, travel through a medium at speeds faster than the speed of light in the medium only then will CR radiate. As the CR occurs, electromagnetic radiation is emitted in a cone shape, fanning out in the forward direction.
CR and the 1937 theory has led to a large array of applications in high energy physics. A notable application are the Cherenkov counters. These are used to determine various properties of a charged particle such as its velocity, charge, direction of motion, and energy. These properties are important in the identification of different particles. For example, the counters were applied in the discovery of the anti-proton and the J particle. Six large Cherenkov counters were used in the discovery of the J particle.
It has been difficult to experimentally prove the reversed Cherenkov radiation.[40][41]
Paraxial approximation of DNG slabs
Theoretical work, along with numerical simulations, began early in the decade of the new millennium on the abilities of the DNG slab for subwavelength focusing. The research began with Pendry's proposed "Perfect lens". Several research investigations that followed Pendry's concluded that the "Perfect lens" was possible in theory but impractical. One direction in subwavelength focusing proceeded with the use of negative index metamaterials, but based on the enhancements for imaging with surface plasmons. In another direction researchers explored paraxial approximations of DNG slabs.[2]
US patent on left-handed composite media
The first US patent granted for a fabricated metamaterial is U.S. Patent 6,791,432, titled "Left handed composite media." The listed inventors are David R. Smith, Sheldon Schultz, Norman Kroll, Richard A. Shelby.
The invention achieves simultaneous negative permittivity and permeability over a common band of frequencies. The material can integrate media which is already composite or continuous, but which will produce negative permittivity and permeability within the same spectrum of frequencies. Different types of continuous or composite may be deemed appropriate when combined for the desired effect. However, the inclusion of a periodic array of conducting elements is preferred. The array scatters electromagnetic radiation at wavelengths longer than the size of the element and lattice spacing. The array is then viewed as an effective medium.[42]
Anomalous dispersion
Propagation of a Gaussian Light Pulse through an Anomalous Dispersion Medium.[43][44] However the speed of transmitting information is always limited to c.[43][45]
Further reading
- J.B. Pendry, A.J. Holden, W.J. Stewart, and I. Youngs, “Extremely low frequency plasmons in metallic mesostructures,” Phys. Rev. Lett., vol. 76, pp. 4773–4776, June 1996. (Free PDF downloads)
- Pendry, J B; Holden, A J; Robbins, D J; Stewart, W J (1998). "Low frequency plasmons in thin-wire structures" (Free PDF downloads). Journal of Physics: Condensed Matter 10 (22): 4785–4809. doi:10.1088/0953-8984/10/22/007. http://esperia.iesl.forth.gr/~ppm/DALHM/bibliography/LHMpdfs/pendry_jocoma10_4785_98.pdf. Also see the Preprint copy.
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. (1999). "Magnetism from conductors and enhanced nonlinear phenomena" (Free PDF download). IEEE Transactions on Microwave Theory and Techniques 47 (11): 2075–2084. doi:10.1109/22.798002. http://people.ee.duke.edu/~drsmith/nim_pubs/pubs_early/Pendry_IEEE_1999.pdf.
- Padilla, Willie J.; Basov, Dimitri N.; Smith, David R. (2006). "Negative refractive index metamaterials" (Free PDF download). Materials Today 9 (7–8): 28. doi:10.1016/S1369-7021(06)71573-5. http://people.ee.duke.edu/~drsmith/pubs_smith_group/padilla_materials_today_2006.pdf.
- Slyusar V.I. Metamaterials on antenna solutions. (Free PDF download). International Conference on Antenna Theory and Techniques, 6–9 October 2009, Lviv, Ukraine.
See also
- History of metamaterials
- Superlens
- Metamaterial cloaking
- Photonic metamaterials
- Metamaterial antennas
- Nonlinear metamaterials
- Photonic crystal
- Seismic metamaterials
- Split-ring resonator
- Acoustic metamaterials
- Metamaterial absorber
- Metamaterial
- Plasmonic metamaterials
- Terahertz metamaterials
- Tunable metamaterials
- Transformation optics
- Theories of cloaking
-
-
-
- Academic journals
-
-
-
-
-
- Metamaterials books
-
-
- Metamaterials Handbook
- Metamaterials: Physics and Engineering Explorations
Metamaterials scientists
- John Pendry
- David R. Smith
- Richard W. Ziolkowski
- Nader Engheta
Institutional research
The research in the field of Metamaterials has diffused out into the American government science research departments, including the US Naval Air Systems Command, US Air Force, and US Army. Many scientific institutions are involved including:
- California Institute of Technology
- University of Colorado at Colorado Springs
- Duke University
- Harvard University
- Helsinki University of Technology
- Iowa State University
- Imperial College London
- Max Planck Society
- National Institute of Standards and Technology
- Nederlandse Organisatie voor Wetenschappelijk Onderzoek[46]
- University College London
- University of California, Berkeley
- University of California, Irvine
- University of California, Los Angeles
- University of California, San Diego
- University of Colorado
- University of Rochester
- Clemson University
Notes
 This article incorporates public domain material from websites or documents of the United States Government. -NIST
This article incorporates public domain material from websites or documents of the United States Government. -NIST- ^ Negative permitivitty was explored in group of research papers which included: Pendry, J.B. et al. "Extremely Low Frequency Plasmons in Metallic Microstructures". Phys. Rev. Lett. 76, 4773 (1996). :Effective permeablitiy with large positive and negative values was explored in the following research: Pendry, J.B. et al. IEEE Trans. Microwave Theory Tech. 47, 2075 (1999).
References
- Mehmet Bayindir et al. Transmission properties of composite metamaterials in free space. Applied Physics Letters. Vol 81Bayindir, Mehmet; Aydin, K.; Ozbay, E.; Markoš, P.; Soukoulis, C. M. (2002-07-01). "Transmission properties of composite metamaterials in free space". Applied Physics Letters 81: 120. Bibcode 2002ApPhL..81..120B. doi:10.1063/1.1492009.
- ^ a b c d e f g h i j k l m Shelby, R. A.; Smith D.R; Shultz S. (2001). "Experimental Verification of a Negative Index of Refraction". Science 292 (5514): 77–79. Bibcode 2001Sci...292...77S. doi:10.1126/science.1058847. PMID 11292865.
- ^ a b c d e f g h Engheta, Nader; Richard W. Ziolkowski (2006-06) (Google Books has this book). Metamaterials: Physics and Engineering Explorations. Wiley & Sons. pp. Chap 1. ISBN 9780471761020.
- ^ a b c d e V. G. Veselago (1968 (Russian text 1967)). "The electrodynamics of substances with simultaneously negative values of ε and μ". Sov. Phys. Usp. 10 (4): 509–14. Bibcode 1968SvPhU..10..509V. doi:10.1070/PU1968v010n04ABEH003699. http://www.physics-online.ru/PaperLogos/1/files/Full_text_English_version.pdf.
- ^ a b c d e f "Three-Dimensional Plasmonic Metamaterials". Plasmonic metamaterial research. The National Institute of Standards and Technology. August 20, 2009. http://www.nist.gov/cnst/nrg/3d_plasmonic_metamaterials.cfm. Retrieved 2011-01-02.This material is in the public domain from an agency of the U.S. Government. For this page, the cited references are as follows:
- Local density of states, spectrum, and far-field interference of surface plasmon polaritons probed by cathodeoluminescence, M. Kuttge, E. J. R. Vesseur, A. F. Koenderink, H. J. Lezec, H. A. Atwater, F. J. Garcia de Abajo, and A. Polman, Physical Review B 79, 113405 (2009).
- Universal Optical Transmission Features in Periodic and Quasiperiodic Hole Arrays, D. Pacifici, H.J. Lezec, L.A. Sweatlock, R.J. Walters, and H.A. Atwater, Optics Express 16(12), 9222 (2008).
- All-optical Modulation by Plasmonic Excitation of CdSe Quantum Dots, D. Pacifici, H.J. Lezec, and H.A. Atwater, Nature Photonics 1(7), 402 (2007).
- Negative Refraction at Visible Frequencies, H.J. Lezec, J.A. Dionne, and H.A. Atwater, Science 316(5823), 430 (2007).
- Diffracted Evanescent Wave Model for Enhanced and Supressed Optical Transmission through Subwavelength Hole Arrays, H.J. Lezec and T. Thio, Optics Express 12(16), 3629 (2004).
- Beaming Light from a Subwavelength Aperture, H.J. Lezec, A. Degiron, E. Devaux, R.A. Linke, L. Martin-Moreno, F.J. Garcia-Vidal, and T.W. Ebbesen, Science 297(5582), 820 (2002).
- ^ A strategy for increasing operational bandwidth to achieve negative index.
- Chevalier, Christine T.; and Wilson, Jeffery D. (November 2004). "Frequency Bandwidth Optimization of Left-Handed Metamaterial". Nasa/tm—2004-213403 (Glenn Research Center). http://gltrs.grc.nasa.gov/reports/2004/TM-2004-213403.pdf. Retrieved 2011-06-11.
- See also http://gltrs.grc.nasa.gov/Citations.aspx?id=1374 Glenn Technical Reports Server.
 This article incorporates public domain material from websites or documents of the National Aeronautics and Space Administration.
This article incorporates public domain material from websites or documents of the National Aeronautics and Space Administration.
- ^ a b c d Shelby, R. A.; Smith D.R.; Shultz S.; Nemat-Nasser S.C. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial". Applied Physics Letters 78 (4): 489. Bibcode 2001ApPhL..78..489S. doi:10.1063/1.1343489. http://people.ee.duke.edu/~drsmith/pubs_smith_group/Shelby_APL_(2001).pdf.
- ^ Boltasseva, A; Shalaev, V (2008). "Fabrication of optical negative-index metamaterials: Recent advances and outlook" (free PDF download). Metamaterials 2: 1–17. doi:10.1016/j.metmat.2008.03.004. http://cobweb.ecn.purdue.edu/~shalaev/Publication_list_files/e6a11dcdfb53727d92491e50a7856ae2.pdf.
- ^ a b Veselago, Viktor G (2003). "Electrodynamics of materials with negative index of refraction" (pay wall). Physics-Uspekhi 46 (7): 764. doi:10.1070/PU2003v046n07ABEH001614. http://iopscience.iop.org/1063-7869/46/7/A11/pdf/1063-7869_46_7_A11.pdf.
- Alternate source at:
- Lim Hock; Ong Chong Kim, and Serguei Matitsine (7 – 12 December 2003). Electromagnetic Materials:. Proceedings of the Symposium F ((ICMAT 2003) ed.). SUNTEC, Singapore: World Scientific. pp. 115–122. ISBN 9789812383723. http://books.google.com/?id=fvzKqPwd098C&pg=PA115#v=onepage&q&f=false. paper by Victor G. Veselago. Electrodynamics of materials with negative index of refraction.
- Alternate source at:
- ^ DOE Pulse. DOE website. Public domain material. 2007.
- ^ Nader Engheta; Ziolkowski, R.W. (2005). "A positive future for double-negative metamaterials" (Free PDF download). IEEE Transactions on Microwave Theory and Techniques 53 (4): 1535. doi:10.1109/TMTT.2005.845188. http://www2.engr.arizona.edu/~ziolkows/research/papers/Metamaterial_Research/Reviews/MTT_April_2005.pdf.
- ^ Beruete, M.; Navarro-Cía, M.; Sorolla, M.; Campillo, I. (2008). "Planoconcave lens by negative refraction of stacked subwavelength hole arrays" (Free PDF download). Optics Express 16 (13): 9677–83. doi:10.1364/OE.16.009677. PMID 18575535. http://www.csm.unavarra.es/Publicaciones/Images/Pub474.pdf.
- ^ Alu, A.; Engheta, N. (2004). "Guided Modes in a Waveguide Filled with a Pair of Single-Negative (SNG), Double-Negative (DNG), and/or Double-Positive (DPS) Layers". IEEE Transactions on Microwave Theory and Techniques 52: 199. doi:10.1109/TMTT.2003.821274.
- ^ a b c Shalaev, Vladimir M. (2007). "Optical negative-index metamaterials" (Free PDF download). Nature Photonics 1: 41. doi:10.1038/nphoton.2006.49. http://ecn.www.ecn.purdue.edu/~photspec/Optical%20negative-index%20metamaterials.pdf.
- ^ a b c d Liu, H. et al. (25 May 2009). "Coupled magnetic plasmons in metamaterials" (PDF download available to the public). Physica Status Solidi B (Nanjing University, U of C Berkley, Lawrence Berkeley National Laboratory) 246 (7): 1397–1406. Bibcode 2009PSSBR.246.1397L. doi:10.1002/pssb.200844414. http://xlab.me.berkeley.edu/publications/pdfs/121.PhysStatSolidiB2009_HuiLiu.pdf. Retrieved 2010-05-04.
- ^ a b c d Padilla, Willie J.; David R. Smith, and Dimitri N. Basov (2006-03-01). "Spectroscopy of metamaterials from infrared to optical frequencies" (First posted on the web 2005-11-07 according to PDF download. Free PDF download.). JOSA B 23 (3): 404–414. Bibcode 2006JOSAB..23..404P. doi:10.1364/JOSAB.23.000404. http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA487502&Location=U2&doc=GetTRDoc.pdf. Retrieved 2010-02-01.
- ^ a b "Physicists invent "left-handed" material". Physicsworld.org (Institute of Physics): p. 01. 2000-03-24. http://physicsworld.com/cws/article/news/2866. Retrieved 2010-02-11.
- ^ Shelby, R. A.; Smith, D. R.; Schultz, S. (2001). "Experimental verification of a negative index of refraction". Science 292 (5514): 77–79. Bibcode 2001Sci...292...77S. doi:10.1126/science.1058847. JSTOR 3082888. PMID 11292865
- ^ a b c d e f g h i j k l m Smith, D. R.; Padilla, Willie; Vier, D.; Nemat-Nasser, S.; Schultz, S. (2000). "Composite Medium with Simultaneously Negative Permeability and Permittivity" (Free PDF download). Physical Review Letters 84 (18): 4184–7. Bibcode 2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. PMID 10990641. http://people.ee.duke.edu/~drsmith/pubs_smith_group/Smith_PRL_84_4184_(2000).pdf.
- ^ a b c McDonald, Kim (2000-03-21). "UCSD Physicists Develop a New Class of Composite Material with 'Reverse' Physical Properties Never Before Seen". UCSD Science and Engineering. http://ucsdnews.ucsd.edu/newsrel/science/mccomposite.htm. Retrieved 2010-12-17.
- ^ Program contact: Carmen Huber (2000-03-21). "Physicist Produce Left Handed Composite Material". National Science Foundation. http://www.nsf.gov/pubs/2000/pr0009/pr0009.txt. Retrieved 2009-07-10.
- ^ Shelby, R. A.; Smith, D. R.; Nemat-Nasser, S. C.; Schultz, S. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial". Applied Physics Letters 78 (4): 489. Bibcode 2001ApPhL..78..489S. doi:10.1063/1.1343489.
- ^ a b Veselago, V. G. (1968). "The electrodynamics of substances with simultaneously negative values of [permittivity] and [permeability]". Soviet Physics Uspekhi 10 (4): 509–514. Bibcode 1968SvPhU..10..509V. doi:10.1070/PU1968v010n04ABEH003699.
- ^ Pennicott, Katie (2001-04-05). "Magic material flips refractive index". Physics World (Institute of Physics). http://physicsworld.com/cws/article/news/2692. Retrieved 2010-02-12.
- ^ Bill Casselman (2009). "The Law of Refraction". University of British Columbia, Canada, Department of Mathematics. http://www.math.ubc.ca/~cass/courses/m309-01a/chu/Fundamentals/snell.htm. Retrieved 2009-07-06.
- ^ L.S. Taylor (2009). "An Anecdotal History of Optics from Aristophanes to Zernike". University of Maryland; Electrical Engineering Department. http://www.ece.umd.edu/~taylor/optics.htm. Retrieved 2009-07-07.
- ^ Ward, David W.; Nelson, Keith A and Webb, Kevin J (2005). "On the physical origins of the negative index of refraction". New Journal of Physics 7 (213): 213. arXiv:physics/0409083. Bibcode 2005NJPh....7..213W. doi:10.1088/1367-2630/7/1/213.
- ^ Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J (1999). "Magnetism from conductors and enhanced nonlinear phenomena". IEEE Transactions on Microwave Theory and Techniques 47 (11): 2075–2084. Bibcode 1999ITMTT..47.2075P. doi:10.1109/22.798002. http://www.cmth.ph.ic.ac.uk/photonics/Newphotonics/pdf/magwires.pdf. Retrieved 2009-07-07.
- ^ "Radar types, principles, bands, hardware". Weather Edge Inc.. 2000. http://www.everythingweather.com/weather-radar/bands.shtml. Retrieved 2009-07-09.
- ^ Parazzoli, C.G. et al. (2003f-03-11). "Experimental Verification and Simulation of Negative Index of Refraction Using Snell's Law" (PDF download available to the public.). Physical Review Letters 90 (10): 107401 (2003) [4 pages]. Bibcode 2003PhRvL..90j7401P. doi:10.1103/PhysRevLett.90.107401. http://capem.buffalo.edu/rashba/PRL07401.pdf. Retrieved 2010-04-19.
- ^ Pacheco, J.; Grzegorczyk, T.; Wu, B.-I.; Zhang, Y.; Kong, J. (2002-12-02). "Power Propagation in Homogeneous Isotropic Frequency-Dispersive Left-Handed Media" (PDF download is available to the public.). Phys. Rev. Lett. 89 (25): 257401 (2002) [4 pages]. Bibcode 2002PhRvL..89y7401P. doi:10.1103/PhysRevLett.89.257401. PMID 12484915. http://web.mit.edu/biwu/www/bib/2002/pacheco_2002_prl.pdf. Retrieved 2010-04-19.
- ^ a b Caloz, C. et al. (2001-12-01). "Full-wave verification of the fundamental properties of left-handed materials in waveguide configurations". Journal of Applied Physics 90 (11): 5483. Bibcode 2001JAP....90.5483C. doi:10.1063/1.1408261. http://xlab.me.berkeley.edu/MURI/publications/publications_9.pdf. Retrieved 2009-12-29.
- ^ a b Ziolkowski, Richard W; and Ehud Heyman (2001-10-30). "Wave propagation in media having negative permittivity and permeability" (Free PDF download. Cited by 506). Physical Review E 64 (5): 056625. Bibcode 2001PhRvE..64e6625Z. doi:10.1103/PhysRevE.64.056625. http://mesoscopic.mines.edu/mediawiki/images/3/3d/Waveprop_DNG_media.pdf. Retrieved 2009-12-30.
- ^ a b Smith, David R.and; Norman Kroll (2000-10-02). "Negative Refractive Index in Left-Handed Materials". Physical Review Letters 85 (14): 2933–2936. Bibcode 2000PhRvL..85.2933S. doi:10.1103/PhysRevLett.85.2933. PMID 11005971. http://www.pi5.uni-stuttgart.de/lehre/wp2001/prl2000-smith.pdf. Retrieved 2010-01-04.
- ^ Srivastava, R. et al. (2008). "Negative refraction by Photonic Crystal" (Free PDF download). Progress in Electromagnetics Research B (PIER B) 2: 15–26. doi:10.2528/PIERB08042302. http://ceta.mit.edu/pierb/pierb02/02.08042302.pdf. Retrieved 2010-01-04.
- ^ Dr. Jamil R. Abo-Shaeer, Program Manager (July 2010). "Negative Index Materials" (Public Domain - Information presented on the DARPA Web Information Service is considered public information and may be distributed or copied. Use of appropriate byline/photo/image credits is requested.). DARPA - Defense Science Offices (DSO). http://www.darpa.mil/dso/thrusts/materials/novelmat/nim/index.htm. Retrieved 2010-07-05.
- ^ Metamaterial studies. Google Scholar. November 2010.
- ^ PhysOrg.com (April 22, 2010). "Novel negative-index metamaterial that responds to visible light designed" (Web page). http://www.physorg.com/news191168001.html. Retrieved 2010-05-05.
- ^ Dillow, Clay (April 23, 2010). "New Metamaterial First to Bend Light in the Visible Spectrum" (Web page). Popular Science. http://www.popsci.com/science/article/2010-04/new-single-layer-metamaterial-bends-light-visbile-spectrum. Retrieved 2010-05-05.
- ^ Caltech Media Relations. Negative Refraction of Visible Light Demonstrated; Could Lead to Cloaking Devices. March 22, 2007. accessdate - 2010-05-05
- ^ Xi, Sheng et al. (2009-11-02). "Experimental Verification of Reversed Cherenkov Radiation in Left-Handed Metamaterial" (Free PDF download). Phys. Rev. Lett. 103 (19): 194801 (2009). Bibcode 2009PhRvL.103s4801X. doi:10.1103/PhysRevLett.103.194801. PMID 20365927. http://physics.aps.org/pdf/10.1103/PhysRevLett.103.194801.pdf. Retrieved 2010-02-24.
- ^ Zhang, Shuang; Xiang Zhang (2009-11-02). "Flipping a photonic shock wave" (Also available in PDF format: Flipping a photonic shock wave). Physics (Viewpoint) (APS) 02 (91): 03. Bibcode 2009PhyOJ...2...91Z. doi:10.1103/Physics.2.91. http://physics.aps.org/articles/v2/91. Retrieved 2010-02-24.
- ^ Smith, David; Schultz, Sheldon; Kroll, Norman; Shelby, Richard A. "Left handed composite media" U.S. Patent 6,791,432 Publication date 2001-03-16, Issue date 2004-03-14.
- ^ a b Dolling, Gunnar; Christian Enkrich, Martin Wegener, Costas M. Soukoulis, Stefan Linden (2006). "Simultaneous Negative Phase and Group Velocity of Light in a Metamaterial". Science 312 (5775): 892–894. Bibcode 2006Sci...312..892D. doi:10.1126/science.1126021. PMID 16690860.
- ^ Garrett, C. G. B.; D. E. McCumber (1969-09-25). "Propagation of a Gaussian Light Pulse through an Anomalous Dispersion Medium". Phys. Rev. A 1 (2): 305–313. Bibcode 1970PhRvA...1..305G. doi:10.1103/PhysRevA.1.305. http://www.physics.princeton.edu/~mcdonald/examples/optics/garrett_pra_1_305_70.pdf.
- ^ Stenner, M. D.; Gauthier, D. J.; Neifeld, M. A. (Oct 2003). "The speed of information in a 'fast-light' optical medium". Nature 425 (6959): 695–8. Bibcode 2003Natur.425..695S. doi:10.1038/nature02016. PMID 14562097.
- ^ "FOM Institute". http://www.fom.nl/live/english/about/introduction_to_FOM.pag.
External links
- Manipulating the Near Field with Metamaterials Slide show, with audio available, by Dr. John Pendry, Imperial College, London
- Laszlo Solymar; Ekaterina Shamonina (2009-03-15). Waves in Metamaterials. Oxford University Press, USA. March 2009.. ISBN 9780199215331. http://books.google.com/?id=014CA0-PaqYC&printsec=frontcover&dq=Waves+in+Metamaterials&cd=1#v=onepage&q=&f=false.
- "Illustrating the Law of Refraction". http://www.math.ubc.ca/~cass/courses/m309-01a/chu/Fundamentals/snell.htm.
- Young, Andrew T. (1999–2009). "An Introduction to Mirages". SDSU San Diego, CA. http://mintaka.sdsu.edu/GF/mirages/mirintro.html. Retrieved 2009-08-12.
- Garrett, C. et al. (1969-09-25). "Light pulse and anamolous dispersion". Phys. Rev. A 1 (2): 305–313. Bibcode 1970PhRvA...1..305G. doi:10.1103/PhysRevA.1.305. http://www.physics.princeton.edu/~mcdonald/examples/optics/garrett_pra_1_305_70.pdf.
- List of science website news stories on Left Handed Materials
- Caloz, Christophe (2009-03). "Perspectives on EM metamaterials" (Full article is available, click on doi link). Materials Today 12 (3): 12–20. doi:10.1016/S1369-7021(09)70071-9.</ref>
Categories:- Metamaterials
- Electromagnetism
- Greek loanwords
- Materials science
- Nanomaterials
- Optical materials
- Theoretical physics
- 2000 in science
- 21st century in science
- 20th century in science
Wikimedia Foundation. 2010.