- Non-uniform rational B-spline
-
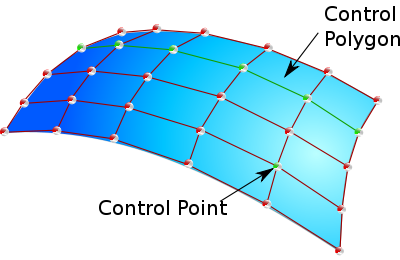
 Three-dimensional NURBS surfaces can have complex, organic shapes. Control points influence the directions the surface takes. The outermost square below delineates the X/Y extents of the surface.
Three-dimensional NURBS surfaces can have complex, organic shapes. Control points influence the directions the surface takes. The outermost square below delineates the X/Y extents of the surface.
Non-uniform rational basis spline (NURBS) is a mathematical model commonly used in computer graphics for generating and representing curves and surfaces which offers great flexibility and precision for handling both analytic and freeform shapes.
Contents
History
Development of NURBS began in the 1950s by engineers who were in need of a mathematically precise representation of freeform surfaces like those used for ship hulls, aerospace exterior surfaces, and car bodies, which could be exactly reproduced whenever technically needed. Prior representations of this kind of surface only existed as a single physical model created by a designer.
The pioneers of this development were Pierre Bézier who worked as an engineer at Renault, and Paul de Casteljau who worked at Citroën, both in France. Bézier worked nearly parallel to de Casteljau, neither knowing about the work of the other. But because Bézier published the results of his work, the average computer graphics user today recognizes splines — which are represented with control points lying off the curve itself — as Bézier splines, while de Casteljau’s name is only known and used for the algorithms he developed to evaluate parametric surfaces. In the 1960s it became clear that non-uniform, rational B-splines are a generalization of Bézier splines, which can be regarded as uniform, non-rational B-splines.
At first NURBS were only used in the proprietary CAD packages of car companies. Later they became part of standard computer graphics packages.
Real-time, interactive rendering of NURBS curves and surfaces was first made available on Silicon Graphics workstations in 1989. In 1993, the first interactive NURBS modeller for PCs, called NöRBS, was developed by CAS Berlin, a small startup company cooperating with the Technical University of Berlin. Today most professional computer graphics applications available for desktop use offer NURBS technology, which is most often realized by integrating a NURBS engine from a specialized company.
Use
NURBS are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE) and are part of numerous industry wide used standards, such as IGES, STEP, ACIS, and PHIGS. NURBS tools are also found in various 3D modeling and animation software packages, such as form•Z, Blender,3ds Max, Maya, Rhino3D, Cinema 4D, Cobalt, Shark FX, and Solid Modeling Solutions. Other than this there are specialized NURBS modeling software packages such as Autodesk Alias Surface, solidThinking and ICEM Surf.
They allow representation of geometrical shapes in a compact form. They can be efficiently handled by the computer programs and yet allow for easy human interaction. NURBS surfaces are functions of two parameters mapping to a surface in three-dimensional space. The shape of the surface is determined by control points.
In general, editing NURBS curves and surfaces is highly intuitive and predictable. Control points are always either connected directly to the curve/surface, or act as if they were connected by a rubber band. Depending on the type of user interface, editing can be realized via an element’s control points, which are most obvious and common for Bézier curves, or via higher level tools such as spline modeling or hierarchical editing.
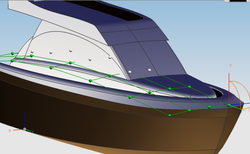
A surface under construction, e.g. the hull of a motor yacht, is usually composed of several NURBS surfaces known as patches. These patches should be fitted together in such a way that the boundaries are invisible. This is mathematically expressed by the concept of geometric continuity.
Higher-level tools exist which benefit from the ability of NURBS to create and establish geometric continuity of different levels:
- Positional continuity (G0)
- holds whenever the end positions of two curves or surfaces are coincidental. The curves or surfaces may still meet at an angle, giving rise to a sharp corner or edge and causing broken highlights.
- Tangential continuity (G1)
- requires the end vectors of the curves or surfaces to be parallel, ruling out sharp edges. Because highlights falling on a tangentially continuous edge are always continuous and thus look natural, this level of continuity can often be sufficient.
- Curvature continuity (G2)
- further requires the end vectors to be of the same length and rate of length change. Highlights falling on a curvature-continuous edge do not display any change, causing the two surfaces to appear as one. This can be visually recognized as “perfectly smooth”. This level of continuity is very useful in the creation of models that require many bi-cubic patches composing one continuous surface.
Geometric continuity mainly refers to the shape of the resulting surface; since NURBS surfaces are functions, it is also possible to discuss the derivatives of the surface with respect to the parameters. This is known as parametric continuity. Parametric continuity of a given degree implies geometric continuity of that degree.
First- and second-level parametric continuity (C0 and C1) are for practical purposes identical to positional and tangential (G0 and G1) continuity. Third-level parametric continuity (C2), however, differs from curvature continuity in that its parameterization is also continuous. In practice, C2 continuity is easier to achieve if uniform B-splines are used.
The definition of the continuity 'Cn' requires that the nth derivative of the curve/surface (dnC(u) / dun) are equal at a joint.[1] Note that the (partial) derivatives of curves and surfaces are vectors that have a direction and a magnitude. Both should be equal.
Highlights and reflections can reveal the perfect smoothing, which is otherwise practically impossible to achieve without NURBS surfaces that have at least G2 continuity. This same principle is used as one of the surface evaluation methods whereby a ray-traced or reflection-mapped image of a surface with white stripes reflecting on it will show even the smallest deviations on a surface or set of surfaces. This method is derived from car prototyping wherein surface quality is inspected by checking the quality of reflections of a neon-light ceiling on the car surface. This method is also known as "Zebra analysis".
Technical specifications
A NURBS curve is defined by its order, a set of weighted control points, and a knot vector. NURBS curves and surfaces are generalizations of both B-splines and Bézier curves and surfaces, the primary difference being the weighting of the control points which makes NURBS curves rational (non-rational B-splines are a special case of rational B-splines). Whereas Bézier curves evolve into only one parametric direction, usually called s or u, NURBS surfaces evolve into two parametric directions, called s and t or u and v.
By evaluating a NURBS curve at various values of the parameter, the curve can be represented in Cartesian two- or three-dimensional space. Likewise, by evaluating a NURBS surface at various values of the two parameters, the surface can be represented in Cartesian space.
NURBS curves and surfaces are useful for a number of reasons:
- They are invariant under affine[2] as well as perspective[3] transformations: operations like rotations and translations can be applied to NURBS curves and surfaces by applying them to their control points.
- They offer one common mathematical form for both standard analytical shapes (e.g., conics) and free-form shapes.
- They provide the flexibility to design a large variety of shapes.
- They reduce the memory consumption when storing shapes (compared to simpler methods).
- They can be evaluated reasonably quickly by numerically stable and accurate algorithms.
In the next sections, NURBS is discussed in one dimension (curves). It should be noted that all of it can be generalized to two or even more dimensions.
Control points
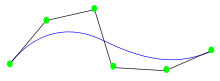
The control points determine the shape of the curve. Typically, each point of the curve is computed by taking a weighted sum of a number of control points. The weight of each point varies according to the governing parameter. For a curve of degree d, the weight of any control point is only nonzero in d+1 intervals of the parameter space. Within those intervals, the weight changes according to a polynomial function (basis functions) of degree d. At the boundaries of the intervals, the basis functions go smoothly to zero, the smoothness being determined by the degree of the polynomial.
As an example, the basis function of degree one is a triangle function. It rises from zero to one, then falls to zero again. While it rises, the basis function of the previous control point falls. In that way, the curve interpolates between the two points, and the resulting curve is a polygon, which is continuous, but not differentiable at the interval boundaries, or knots. Higher degree polynomials have correspondingly more continuous derivatives. Note that within the interval the polynomial nature of the basis functions and the linearity of the construction make the curve perfectly smooth, so it is only at the knots that discontinuity can arise.
The fact that a single control point only influences those intervals where it is active is a highly desirable property, known as local support. In modeling, it allows the changing of one part of a surface while keeping other parts equal.
Adding more control points allows better approximation to a given curve, although only a certain class of curves can be represented exactly with a finite number of control points. NURBS curves also feature a scalar weight for each control point. This allows for more control over the shape of the curve without unduly raising the number of control points. In particular, it adds conic sections like circles and ellipses to the set of curves that can be represented exactly. The term rational in NURBS refers to these weights.
The control points can have any dimensionality. One-dimensional points just define a scalar function of the parameter. These are typically used in image processing programs to tune the brightness and color curves. Three-dimensional control points are used abundantly in 3D modeling, where they are used in the everyday meaning of the word 'point', a location in 3D space. Multi-dimensional points might be used to control sets of time-driven values, e.g. the different positional and rotational settings of a robot arm. NURBS surfaces are just an application of this. Each control 'point' is actually a full vector of control points, defining a curve. These curves share their degree and the number of control points, and span one dimension of the parameter space. By interpolating these control vectors over the other dimension of the parameter space, a continuous set of curves is obtained, defining the surface.
The knot vector
The knot vector is a sequence of parameter values that determines where and how the control points affect the NURBS curve. The number of knots is always equal to the number of control points plus curve degree plus one. The knot vector divides the parametric space in the intervals mentioned before, usually referred to as knot spans. Each time the parameter value enters a new knot span, a new control point becomes active, while an old control point is discarded. It follows that the values in the knot vector should be in nondecreasing order, so (0, 0, 1, 2, 3, 3) is valid while (0, 0, 2, 1, 3, 3) is not.
Consecutive knots can have the same value. This then defines a knot span of zero length, which implies that two control points are activated at the same time (and of course two control points become deactivated). This has impact on continuity of the resulting curve or its higher derivatives; for instance, it allows the creation of corners in an otherwise smooth NURBS curve. A number of coinciding knots is sometimes referred to as a knot with a certain multiplicity. Knots with multiplicity two or three are known as double or triple knots. The multiplicity of a knot is limited to the degree of the curve; since a higher multiplicity would split the curve into disjoint parts and it would leave control points unused. For first-degree NURBS, each knot is paired with a control point.
The knot vector usually starts with a knot that has multiplicity equal to the order. This makes sense, since this activates the control points that have influence on the first knot span. Similarly, the knot vector usually ends with a knot of that multiplicity. Curves with such knot vectors start and end in a control point.
The individual knot values are not meaningful by themselves; only the ratios of the difference between the knot values matter. Hence, the knot vectors (0, 0, 1, 2, 3, 3) and (0, 0, 2, 4, 6, 6) produce the same curve. The positions of the knot values influences the mapping of parameter space to curve space. Rendering a NURBS curve is usually done by stepping with a fixed stride through the parameter range. By changing the knot span lengths, more sample points can be used in regions where the curvature is high. Another use is in situations where the parameter value has some physical significance, for instance if the parameter is time and the curve describes the motion of a robot arm. The knot span lengths then translate into velocity and acceleration, which are essential to get right to prevent damage to the robot arm or its environment. This flexibility in the mapping is what the phrase non uniform in NURBS refers to.
Necessary only for internal calculations, knots are usually not helpful to the users of modeling software. Therefore, many modeling applications do not make the knots editable or even visible. It's usually possible to establish reasonable knot vectors by looking at the variation in the control points. More recent versions of NURBS software (e.g., Autodesk Maya and Rhinoceros 3D) allow for interactive editing of knot positions, but this is significantly less intuitive than the editing of control points.
Order
The order of a NURBS curve defines the number of nearby control points that influence any given point on the curve. The curve is represented mathematically by a polynomial of degree one less than the order of the curve. Hence, second-order curves (which are represented by linear polynomials) are called linear curves, third-order curves are called quadratic curves, and fourth-order curves are called cubic curves. The number of control points must be greater than or equal to the order of the curve.
In practice, cubic curves are the ones most commonly used. Fifth- and sixth-order curves are sometimes useful, especially for obtaining continuous higher order derivatives, but curves of higher orders are practically never used because they lead to internal numerical problems and tend to require disproportionately large calculation times.
Construction of the basis functions[4]
The basis functions used in NURBS curves are usually denoted as Ni,n(u), in which i corresponds to the i-th control point, and n corresponds with the degree of the basis function. The parameter dependence is frequently left out, so we can write Ni,n. The definition of these basis functions is recursive in n. The degree-0 functions Ni,0 are piecewise constant functions. They are one on the corresponding knot span and zero everywhere else. Effectively, Ni,n is a linear interpolation of Ni,n − 1 and Ni + 1,n − 1. The latter two functions are non-zero for n knot spans, overlapping for n − 1 knot spans. The function Ni,n is computed as
 From bottom to top: Linear basis functions N1,1 (blue) and N2,1 (green), their weight functions f and g and the resulting quadratic basis function. The knots are 0, 1, 2 and 2.5
From bottom to top: Linear basis functions N1,1 (blue) and N2,1 (green), their weight functions f and g and the resulting quadratic basis function. The knots are 0, 1, 2 and 2.5- Ni,n = fi,nNi,n − 1 + gi + 1,nNi + 1,n − 1
fi rises linearly from zero to one on the interval where Ni,n − 1 is non-zero, while gi + 1 falls from one to zero on the interval where Ni + 1,n − 1 is non-zero. As mentioned before, Ni,1 is a triangular function, nonzero over two knot spans rising from zero to one on the first, and falling to zero on the second knot span. Higher order basis functions are non-zero over corresponding more knot spans and have correspondingly higher degree. If u is the parameter, and ki is the i-th knot, we can write the functions f and g as
and
The functions f and g are positive when the corresponding lower order basis functions are non-zero. By induction on n it follows that the basis functions are non-negative for all values of n and u. This makes the computation of the basis functions numerically stable.
Again by induction, it can be proved that the sum of the basis functions for a particular value of the parameter is unity. This is known as the partition of unity property of the basis functions.
 Linear basis functions
Linear basis functions Quadratic basis functions
Quadratic basis functionsThe figures show the linear and the quadratic basis functions for the knots {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1, ...}
One knot span is considerably shorter than the others. On that knot span, the peak in the quadratic basis function is more distinct, reaching almost one. Conversely, the adjoining basis functions fall to zero more quickly. In the geometrical interpretation, this means that the curve approaches the corresponding control point closely. In case of a double knot, the length of the knot span becomes zero and the peak reaches one exactly. The basis function is no longer differentiable at that point. The curve will have a sharp corner if the neighbour control points are not collinear.
General form of a NURBS curve
Using the definitions of the basis functions Ni,n from the previous paragraph, a NURBS curve takes the following form[5]:
In this, k is the number of control points
 and wi are the corresponding weights. The denominator is a normalizing factor that evaluates to one if all weights are one. This can be seen from the partition of unity property of the basis functions. It is customary to write this as
and wi are the corresponding weights. The denominator is a normalizing factor that evaluates to one if all weights are one. This can be seen from the partition of unity property of the basis functions. It is customary to write this asin which the functions
are known as the rational basis functions.
Manipulating NURBS objects
A number of transformations can be applied to a NURBS object. For instance, if some curve is defined using a certain degree and N control points, the same curve can be expressed using the same degree and N+1 control points. In the process a number of control points change position and a knot is inserted in the knot vector. These manipulations are used extensively during interactive design. When adding a control point, the shape of the curve should stay the same, forming the starting point for further adjustments. A number of these operations are discussed below.[6]
Knot insertion
As the term suggests, knot insertion inserts a knot into the knot vector. If the degree of the curve is n, then n − 1 control points are replaced by n new ones. The shape of the curve stays the same.
A knot can be inserted multiple times, up to the maximum multiplicity of the knot. This is sometimes referred to as knot refinement and can be achieved by an algorithm that is more efficient than repeated knot insertion.
Knot removal
Knot removal is the reverse of knot insertion. Its purpose is to remove knots and the associated control points in order to get a more compact representation. Obviously, this is not always possible while retaining the exact shape of the curve. In practice, a tolerance in the accuracy is used to determine whether a knot can be removed. The process is used to clean up after an interactive session in which control points may have been added manually, or after importing a curve from a different representation, where a straightforward conversion process leads to redundant control points.
Degree elevation
A NURBS curve of a particular degree can always be represented by a NURBS curve of higher degree. This is frequently used when combining separate NURBS curves, e.g. when creating a NURBS surface interpolating between a set of NURBS curves or when unifying adjacent curves. In the process, the different curves should be brought to the same degree, usually the maximum degree of the set of curves. The process is known as degree elevation.
Curvature
The most important property in differential geometry is the curvature κ. It describes the local properties (edges, corners, etc.) and relations between the first and second derivative, and thus, the precise curve shape. Having determined the derivatives it is easy to compute
 or approximated as the arclength from the second derivate κ = | r''(so) | . The direct computation of the curvature κ with these equations is the big advantage of parameterized curves against their polygonal representations.
or approximated as the arclength from the second derivate κ = | r''(so) | . The direct computation of the curvature κ with these equations is the big advantage of parameterized curves against their polygonal representations.Example: a circle
Non-rational splines or Bézier curves may approximate a circle, but they cannot represent it exactly. Rational splines can represent any conic section, including the circle, exactly. This representation is not unique, but one possibility appears below:
x y z weight 1 0 0 1 1 1 0 
0 1 0 1 −1 1 0 
−1 0 0 1 −1 −1 0 
0 −1 0 1 1 −1 0 
1 0 0 1 The order is two, since a circle is a quadratic curve and the spline's order is one more than the degree of its piecewise polynomial segments. The knot vector is
 . The circle is composed of four quarter circles, tied together with double knots. Although double knots in a third order NURBS curve would normally result in loss of continuity in the first derivative, the control points are positioned in such a way that the first derivative is continuous. (In fact, the curve is infinitely differentiable everywhere, as it must be if it exactly represents a circle.)
. The circle is composed of four quarter circles, tied together with double knots. Although double knots in a third order NURBS curve would normally result in loss of continuity in the first derivative, the control points are positioned in such a way that the first derivative is continuous. (In fact, the curve is infinitely differentiable everywhere, as it must be if it exactly represents a circle.)The curve represents a circle exactly, but it is not exactly parametrized in the circle's arc length. This means, for example, that the point at t does not lie at (sin(t),cos(t)) (except for the start, middle and end point of each quarter circle, since the representation is symmetrical). This is obvious; the x coordinate of the circle would otherwise provide an exact rational polynomial expression for cos(t), which is impossible. The circle does make one full revolution as its parameter t goes from 0 to 2π, but this is only because the knot vector was arbitrarily chosen as multiples of π / 2.
See also
- Spline
- Bézier surface
- de Boor's algorithm
- Subdivision surface
- Triangle mesh
- Point cloud
- Rational motion
- Isogeometric analysis
References
- Les Piegl & Wayne Tiller: The NURBS Book, Springer-Verlag 1995–1997 (2nd ed.). The main reference for Bézier, B-Spline and NURBS; chapters on mathematical representation and construction of curves and surfaces, interpolation, shape modification, programming concepts.
- Dr. Thomas Sederberg, BYU NURBS, http://cagd.cs.byu.edu/~557/text/ch6.pdf
- Dr. Lyle Ramshaw. Blossoming: A connect-the-dots approach to splines, Research Report 19, Compaq Systems Research Center, Palo Alto, CA, June 1987
- David F. Rogers: An Introduction to NURBS with Historical Perspective, Morgan Kaufmann Publishers 2001. Good elementary book for NURBS and related issues.
Notes
- ^ Foley, van Dam, Feiner & Hughes: Computer Graphics: Principles and Practice, section 11.2, Addison Wesley 1996 (2nd ed.).
- ^ David F. Rogers: An Introduction to NURBS with Historical Perspective, section 7.1
- ^ Demidov, Evgeny. "NonUniform Rational B-splines (NURBS) - Perspective projection". An Interactive Introduction to Splines. Ibiblio. http://www.ibiblio.org/e-notes/Splines/NURBS.htm. Retrieved 2010-02-14.
- ^ Les Piegl & Wayne Tiller: The NURBS Book, chapter 2, sec. 2
- ^ Les Piegl & Wayne Tiller: The NURBS Book, chapter 4, sec. 2
- ^ Les Piegl & Wayne Tiller: The NURBS Book, chapter 5
External links
- About Nonuniform Rational B-Splines - NURBS
- An Interactive Introduction to Splines
- http://www.cs.bris.ac.uk/Teaching/Resources/COMS30115/all.pdf
- http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV0405/DONAVANIK/bezier.html
- http://mathcs.holycross.edu/~croyden/csci343/notes.html (Lecture 33: Bézier Curves, Splines)
- http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/notes.html
- A free software package for handling NURBS curves, surfaces and volumes in Octave and Matlab
Wikimedia Foundation. 2010.