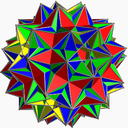
- Uniform star polyhedron
-
 A display of uniform polyhedra at the Science Museum in London
A display of uniform polyhedra at the Science Museum in London
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures or both.
The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 5 quasiregular ones, and 48 semiregular ones.
There are also two infinite sets of uniform star prisms and uniform star antiprisms.
Just as (nondegenerate) star polygons (which have Polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 48 nonprismatic such uniform star polyhedra. The remaining 9 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra, and do not correspond to spherical polyhedra, as the center cannot be projected uniquely onto the sphere.
The nonconvex forms are constructed from Schwarz triangles.
All the uniform polyhedra are listed below by their symmetry groups and subgrouped by their vertex arrangements.
Regular polyhedra are labeled by their Schläfli symbol. Other nonregular uniform polyhedra are listed with their vertex configuration or their Uniform polyhedron index U(1-80).
Note: For nonconvex forms below an additional descriptor Nonuniform is used when the convex hull vertex arrangement has same topology as one of these, but has nonregular faces. For example an nonuniform cantellated form may have rectangles created in place of the edges rather than squares.
Contents
Dihedral symmetry
See Prismatic uniform polyhedron.
Tetrahedral symmetry
There are two nonconvex forms, the tetrahemihexahedron and octahemioctahedron which have tetrahedral symmetry (with fundamental domain Mobius triangle (3 3 2)).
There are two Schwarz triangles that generate unique nonconvex uniform polyhedra: one right triangle (3/2 3 2), and one general triangle (3/2 3 3).
Vertex arrangement
(Convex hull)Nonconvex forms 
Tetrahedron
Rectified tetrahedron
Octahedron
(4.3/2.4.3)
3/2 3 | 2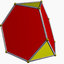
Truncated tetrahedron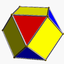
Cantellated tetrahedron
(Cuboctahedron)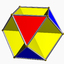
(6.3/2.6.3)
3/2 3 | 3
Omnitruncated tetrahedron
(Truncated octahedron)
Snub tetrahedron
(Icosahedron)Octahedral symmetry
There are 8 convex forms, and 10 nonconvex forms with octahedral symmetry (with fundamental domain Mobius triangle (4 3 2)).
There are four Schwarz_triangles that generate nonconvex forms, two right triangles (3/2 4 2), and (4/3 3 2), and two general triangles: (4/3 4 3), (3/2 4 4).
Vertex arrangement
(Convex hull)Nonconvex forms 
Cube
Octahedron
Cuboctahedron
(6.4/3.6.4)
4/3 4 | 3
Truncated cube
(4.8/3.4/3.8/5)
2 4/3 (3/2 4/2) |
(8/3.3.8/3.4)
3 4 | 4/3
(4.3/2.4.4)
3/2 4 | 2
Truncated octahedron
Rhombicuboctahedron
(4.8.4/3.8)
2 4 (3/2 4/2) |
(8.3/2.8.4)
3/2 4 | 4
(8/3.8/3.3)
2 3 | 4/3
Nonuniform
truncated cuboctahedron
(4.6.8/3)
2 3 4/3 |
Nonuniform
truncated cuboctahedron
(8/3.6.8)
3 4 4/3 |
Snub cubeIcosahedral symmetry
There are 8 convex forms and 46 nonconvex forms with icosahedral symmetry (with fundamental domain Mobius triangle (5 3 2)). (or 47 nonconvex forms if Skilling's figure is included). Some of the nonconvex snub forms have reflective vertex symmetry.
Vertex arrangement
(Convex hull)Nonconvex forms 
{5/2,5}
{5,5/2}
{3,5/2}
Nonuniform
truncated icosahedron
2 5 |3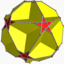
U37
2 5/2 | 5
U61
5/2 3 | 5/3
U67
5/3 3 | 2
U73
2 5/3 (3/2 5/4) |
Nonuniform
truncated icosahedron
2 5 |3
U38
5/2 5 | 2
U44
5/3 5 | 3
U56
2 3 (5/4 5/2) |
Nonuniform
truncated icosahedron
2 5 |3
U32
| 5/2 3 3
Icosidodecahedron
2 | 3 5
U49
3/2 3 | 5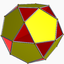
U51
5/4 5 | 5
U54
2 | 3 5/2
U70
5/3 5/2 | 5/3
U71
3 3 | 5/3
U36
2 | 5 5/2
U62
5/3 5/2 | 3
U65
5/4 5 | 3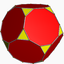
Truncated dodecahedron
2 3 | 5
U42
U48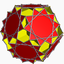
U63
Nonuniform
truncated dodecahedron
U72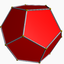
Dodecahedron
{5/2,3}
U30
U41
U47
Rhombicosidodecahedron
U33
U39
U58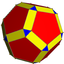
Beveled
Dodecahedron
U55
Nonuniform
rhombicosidodecahedron
U31
U43
U50
U66
Nonuniform
rhombicosidodecahedron
U75
U64
Skilling's figure
(see below)
Nonuniform
truncated icosidodecahedron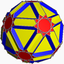
U45
Nonuniform
truncated icosidodecahedron
U59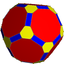
Nonuniform
truncated icosidodecahedron
U68
Nonuniform
snub dodecahedron
U40
U46
U57
U69
U60
U74Skilling's figure
One further nonconvex polyhedron is the Great disnub dirhombidodecahedron, also known as Skilling's figure, which is vertex-uniform, but has pairs of edges which coincide in space such that four faces meet at some edges. It is sometimes but not always counted as a uniform polyhedron. It has Ih symmetry.
Degenerate cases
Coxeter identified a number of degenerate star polyhedra by the Wythoff construction method, which contain overlapping edges or vertices. These degenerate forms include:
- Small complex icosidodecahedron
- Great complex icosidodecahedron
See also
Notes
References
- Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 246 (916): 401–450. doi:10.1098/rsta.1954.0003.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
- Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [1]
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR0062446
- Sopov, S. P. (1970), "A proof of the completeness on the list of elementary homogeneous polyhedra", Ukrainskiui Geometricheskiui Sbornik (8): 139–156, MR0326550
- Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 278: 111–135, ISSN 0080-4614, JSTOR 74475, MR0365333
- Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
- Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [2]
- Messer, Peter W. Closed-Form Expressions for Uniform Polyhedra and Their Duals., Discrete & Computational Geometry 27:353-375 (2002).
- Richard Klitzing, 3D, uniform polyhedra
External links
Categories:- Uniform polyhedra
Wikimedia Foundation. 2010.