- Bayesian network
-
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph (DAG). For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
Formally, Bayesian networks are directed acyclic graphs whose nodes represent random variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes which are not connected represent variables which are conditionally independent of each other. Each node is associated with a probability function that takes as input a particular set of values for the node's parent variables and gives the probability of the variable represented by the node. For example, if the parents are m Boolean variables then the probability function could be represented by a table of 2m entries, one entry for each of the 2m possible combinations of its parents being true or false.
Efficient algorithms exist that perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.
Contents
Definitions and concepts
There are several equivalent definitions of a Bayesian network. For all the following, let G = (V,E) be a directed acyclic graph (or DAG), and let X = (Xv)v ∈ V be a set of random variables indexed by V.
Factorization definition
X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:[1]

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).
For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:[1]

Compare this with the definition above, which can be written as:
 for each
for each  which is a parent of
which is a parent of 
The difference between the two expressions is the conditional independence of the variables from any of their non-descendents, given the values of their parent variables.
Local Markov property
X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:[2]
where de(v) is the set of descendants of v.
This can also be expressed in terms similar to the first definition, as
 for each
for each  which is not a descendent of
which is not a descendent of  for each
for each  which is a parent of
which is a parent of 
Note that the set of parents is a subset of the set of non-descendants because the graph is acyclic.
Developing Bayesian networks
To develop a Bayesian network, we often first develop a DAG G such that we believe X satisfies the local Markov property with respect to G. Sometimes this is done by creating a causal DAG. We then ascertain the conditional probability distributions of each variable given its parents in G. In many cases, in particular in the case where the variables are discrete, if we define the joint distribution of X to be the product of these conditional distributions, then X is a Bayesian network with respect to G.[3]
Markov blanket
The Markov blanket of a node is its set of neighboring nodes: its parents, its children, and any other parents of its children. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.[2]
d-separation
This definition can be made more general by defining the "d"-separation of two nodes, where d stands for directional.[4] Let P be a trail (that is, a path which can go in either direction) from node u to v. Then P is said to be d-separated by a set of nodes Z if and only if (at least) one of the following holds:
- P contains a chain, i → m → j, such that the middle node m is in Z,
- P contains a chain, i ← m ← j, such that the middle node m is in Z,
- P contains a fork, i ← m → j, such that the middle node m is in Z, or
- P contains an inverted fork (or collider), i → m ← j, such that the middle node m is not in Z and no descendant of m is in Z.
Thus u and v are said to be d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are called d-connected.
X is a Bayesian network with respect to G if, for any two nodes u, v:
where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)
Causal networks
Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that Xv is causally dependent on Xu. This is demonstrated by the fact that Bayesian networks on the graphs:
are equivalent: that is they impose exactly the same conditional independence requirements.
A causal network is a Bayesian network with an explicit requirement that the relationships be causal. The additional semantics of the causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X=x)), then the probability density function changes to the one of the network obtained by cutting the links from X's parents to X, and setting X to the caused value x.[5] Using these semantics, one can predict the impact of external interventions from data obtained prior to intervention.
Example
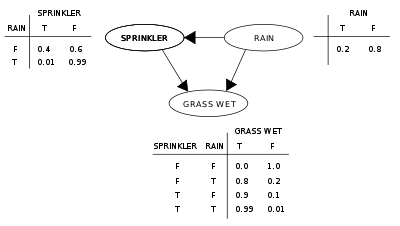
Suppose that there are two events which could cause grass to be wet: either the sprinkler is on or it's raining. Also, suppose that the rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler is usually not turned on). Then the situation can be modeled with a Bayesian network (shown). All three variables have two possible values, T (for true) and F (for false).
The joint probability function is:
- P(G,S,R) = P(G | S,R)P(S | R)P(R)
where the names of the variables have been abbreviated to G = Grass wet, S = Sprinkler, and R = Rain.
The model can answer questions like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:
As in the example numerator is pointed out explicitly, the joint probability function is used to calculate each iteration of the summation function. In the numerator marginalizing over S and in the denominator marginalizing over S and R.
If, on the other hand, we wish to answer an interventional question: "What is the likelihood that it would rain, given that we wet the grass?" the answer would be governed by the post-intervention joint distribution function P(S,R | do(G = T)) = P(S | R)P(R) obtained by removing the factor P(G | S,R) from the pre-intervention distribution. As expected, the likelihood of rain is unaffected by the action: P(R | do(G = T)) = P(R).
If, moreover, we wish to predict the impact of turning the sprinkler on, we have P(R,G | do(S = T)) = P(R)P(G | R,S = T) with the term P(S = T | R) removed, showing that the action has an effect on the grass but not on the rain.
These predictions may not be feasible when some of the variables are unobserved, as in most policy evaluation problems. The effect of the action do(x) can still be predicted, however, whenever a criterion called "back-door" is satisfied.[5] It states that, if a set Z of nodes can be observed that d-separates (or blocks) all back-door paths from X to Y then P(Y,Z | do(x)) = P(Y,Z,X = x) / P(X = x | Z). A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called "sufficient" or "admissible." For example, the set Z=R is admissible for predicting the effect of S=T on G, because R d-separate the (only) back-door path S←R→G. However, if S is not observed, there is no other set that d-separates this path and the effect of turning the sprinkler on (S=T) on the grass (G) cannot be predicted from passive observations. We then say that P(G|do(S=T)) is not "identified." This reflects the fact that, lacking interventional data, we cannot determine if the observed dependence between S and G is due to a causal connection or due to spurious created by a common cause, R. (see Simpson's paradox)
Using a Bayesian network can save considerable amounts of memory, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for 210 = 1024 values. If the local distributions of no variable depends on more than 3 parent variables, the Bayesian network representation only needs to store at most 10 * 23 = 80 values.
One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distribution.
Inference and learning
There are three main inference tasks for Bayesian networks.
Inferring unobserved variables
Because a Bayesian network is a complete model for the variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to find out updated knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when one wants to choose values for the variable subset which minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.
The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space-time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation, and variational methods.
Parameter learning
In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon X's parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, one commonly specifies the conditional distribution for the hidden state's temporal evolution to maximize the entropy rate of the implied stochastic process.)
Often these conditional distributions include parameters which are unknown and must be estimated from data, sometimes using the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex when there are unobserved variables. A classical approach to this problem is the expectation-maximization algorithm which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.
A more fully Bayesian approach to parameters is to treat parameters as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, so in practice classical parameter-setting approaches are more common.
Structure learning
In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.
Automatically learning the graph structure of a Bayesian network is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl (1987)[6] and rests on the distinction between the three possible types of adjacent triplets allowed in a directed acyclic graph (DAG):
Type 1 and type 2 represent the same dependencies (X and Z are independent given Y) and are, therefore, indistinguishable. Type 3, however, can be uniquely identified, since X and Z are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when X and Z have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independencies observed.[5][7][8][9]
An alternative method of structural learning uses optimization based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data. The time requirement of an exhaustive search returning back a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al.[citation needed] talk about using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.
Applications
Bayesian networks are used for modelling knowledge in computational biology and bioinformatics (gene regulatory networks, protein structure, gene expression analysis[10]), medicine,[11] document classification, information retrieval,[12] image processing, data fusion, decision support systems,[13] engineering, gaming and law.[14][15][16]
History
The term "Bayesian networks" was coined by Judea Pearl in 1985 to emphasize three aspects:[17]
- The often subjective nature of the input information.
- The reliance on Bayes's conditioning as the basis for updating information.
- The distinction between causal and evidential modes of reasoning, which underscores Thomas Bayes' posthumously published paper of 1763.[18]
In the late 1980s the seminal texts Probabilistic Reasoning in Intelligent Systems[19] and Probabilistic Reasoning in Expert Systems[20] summarized the properties of Bayesian networks and helped to establish Bayesian networks as a field of study.
Informal variants of such networks were first used by legal scholar John Henry Wigmore, in the form of Wigmore charts, to analyse trial evidence in 1913.[15]:66–76 Another variant, called path diagrams, was developed by the geneticist Sewall Wright[21] and used in social and behavioral sciences (mostly with linear parametric models).
See also
- Artificial intelligence
- Bayes' theorem
- Dempster–Shafer theory – a Generalization of Bayes' theorem
- Bayesian inference
- Bayesian probability
- Belief propagation
- Chow–Liu tree
- Computational intelligence
- Computational phylogenetics
- Dynamic Bayesian network
- Expectation-maximization algorithm
- Graphical model
- Hierarchical temporal memory
- Influence diagram
- José-Miguel Bernardo
- Judea Pearl
- Kalman filter
- Machine learning
- Memory prediction framework
- Naive Bayes classifier
- Path analysis
- Polytree
- Sensor fusion
- Sequence alignment
- Speech recognition
- Structural equation modeling
- Subjective logic
- Variable-order Bayesian network
- Wigmore chart
- World view
Notes
- ^ a b Russell & Norvig 2003, p. 496.
- ^ a b Russell & Norvig 2003, p. 499.
- ^ Neapolitan, R.E.,Learning Bayesian Networks, Prentice Hall, Upper Saddle River, NJ, 2004
- ^ Geiger, Dan; Verma, Thomas and Pearl, Judea (1990). "Identifying independence in Bayesian Networks". Networks 20: 507-534. http://ftp.cs.ucla.edu/pub/stat_ser/r116.pdf. Retrieved 6 October 2011.
- ^ a b c Pearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press. ISBN 0-521-77362-8.
- ^ Rebane, G. and Pearl, J., "The Recovery of Causal Poly-trees from Statistical Data," Proceedings, 3rd Workshop on Uncertainty in AI, (Seattle, WA) pages 222–228, 1987
- ^ P. Spirtes and C. Glymour, "An algorithm for fast recovery of sparse causal graphs", Social Science Computer Review, Vol. 9, pages 62–72, 1991.
- ^ P. Spirtes, C. Glymour, and R. Scheines, Causation, Prediction, and Search, New York: Springer-Verlag, 1993
- ^ T. Verma and J. Pearl, "Equivalence and Synthesis of Causal Models," Proceedings of the Sixth Conference on Uncertainty in Artificial Intelligence, (July, Cambridge, MA), pages 220–227, 1990. Reprinted in P. Bonissone, M. Henrion, L. N. Kanal and J. F. Lemmer (editors), Uncertainty in Artificial Intelligence 6, Amsterdam: Elsevier Science Publishers, B.V., pages 225–268, 1991
- ^ N. Friedman, M. Linial, I. Nachman, D. Pe'er (August 2000). "Using Bayesian Networks to Analyze Expression Data". Journal of Computational Biology (Larchmont, New York: Mary Ann Liebert, Inc.) 7 (3/4): 601–620. doi:10.1089/106652700750050961. ISSN 1066-5277. PMID 11108481.
- ^ J. Uebersax (2004). Genetic Counseling and Cancer Risk Modeling: An Application of Bayes Nets. Marbella, Spain: Ravenpack International. http://www.john-uebersax.com/stat/bayes_net_breast_cancer.doc.
- ^ Luis M. de Campos, Juan M. Fernández-Luna and Juan F. Huete (2004). "Bayesian networks and information retrieval: an introduction to the special issue". Information Processing & Management (Elsevier) 40 (5): 727–733. doi:10.1016/j.ipm.2004.03.001. ISBN 0-471-14182-8.
- ^ F.J. Díez and F. J. D'iez and J. Mira and E. Iturralde and S. Zubillaga (1997). "DIAVAL, a Bayesian expert system for echocardiography". Artificial Intelligence in Medicine (Elsevier Science B.V) 10 (1): 59–73. doi:10.1016/S0933-3657(97)00384-9. PMID 9177816.
- ^ G. A. Davis (2003). "Bayesian reconstruction of traffic accidents". Law, Probability and Risk 2 (2): 69–89. doi:10.1093/lpr/2.2.69.
- ^ a b J. B. Kadane and D. A. Schum (1996). A Probabilistic Analysis of the Sacco and Vanzetti Evidence. New York: Wiley. ISBN 0-471-14182-8.
- ^ O. Pourret, P. Naim and B. Marcot (2008). Bayesian Networks: A Practical Guide to Applications. Chichester, UK: Wiley. ISBN 978-0-470-06030-8. http://www.wiley.com/go/pourret.
- ^ Pearl, J. (1985). "Bayesian Networks: A Model of Self-Activated Memory for Evidential Reasoning" (UCLA Technical Report CSD-850017). Proceedings of the 7th Conference of the Cognitive Science Society, University of California, Irvine, CA. pp. 329–334. http://ftp.cs.ucla.edu/tech-report/198_-reports/850017.pdf. Retrieved 2009-05-01.
- ^ Bayes, T.; Price, Mr. (1763). "An Essay towards solving a Problem in the Doctrine of Chances". Philosophical Transactions of the Royal Society of London 53: 370–418. doi:10.1098/rstl.1763.0053.
- ^ Pearl, J., Probabilistic Reasoning in Intelligent Systems, Morgan Kaufmann, San Francisco, CA, 1988
- ^ Neapolitan, R.E., Probabilistic Reasoning in Expert Systems, Wiley, NY, 1989
- ^ Wright, S. (1921). "Correlation and Causation". Journal of Agricultural Research 20 (7): 557–585. http://www.ssc.wisc.edu/soc/class/soc952/Wright/Wright_Correlation%20and%20Causation.pdf.
General references
- Ben-Gal, Irad (2007). "Encyclopedia of Statistics in Quality and Reliability". In Ruggeri, Fabrizio; Kennett, Ron S.; Faltin, Frederick W. Encyclopedia of Statistics in Quality and Reliability. John Wiley & Sons. doi:10.1002/9780470061572.eqr089. ISBN 978-0-470-01861-3. http://www.eng.tau.ac.il/~bengal/BN.pdf.
- Borgelt, Christian; Kruse, Rudolf (March 2002). Graphical Models: Methods for Data Analysis and Mining. Chichester, UK: Wiley. ISBN 0-470-84337-3. http://fuzzy.cs.uni-magdeburg.de/books/gm/.
- Borsuk, Mark Edward (2008). "Ecological informatics: Bayesian networks". In Jørgensen , Sven Erik, Fath, Brian. Encyclopedia of Ecology. Elsevier. ISBN 978-0-444-52033-3.
- Castillo, Enrique; Gutiérrez, José Manuel; Hadi, Ali S. (1997). "Learning Bayesian Networks". Expert Systems and Probabilistic Network Models. Monographs in computer science. New York: Springer-Verlag. pp. 481–528. ISBN 0-387-94858-9.
- Comley, Joshua W.; Dowe, David L. (October 2003). "Minimum Message Length and Generalized Bayesian Nets with Asymmetric Languages". written at Victoria, Australia. In Grünwald, Peter D.; Myung, In Jae; Pitt, Mark A.. Advances in Minimum Description Length: Theory and Applications. Neural information processing series. Cambridge, Massachusetts: Bradford Books (MIT Press). April 2005. pp. 265–294. ISBN 0-262-07262-9. http://www.csse.monash.edu.au/~dld/David.Dowe.publications.html#ComleyDowe2005. (This paper puts decision trees in internal nodes of Bayes networks using Minimum Message Length (MML). An earlier version is Comley and Dowe (2003), .pdf.)
- Dowe, David L. (2010). MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness, in Handbook of Philosophy of Science (Volume 7: Handbook of Philosophy of Statistics), Elsevier, ISBN 978-0-444-51862-0, pp 901-982.
- Fenton, Norman; Neil, Martin E. (November 2007). Managing Risk in the Modern World: Applications of Bayesian Networks – A Knowledge Transfer Report from the London Mathematical Society and the Knowledge Transfer Network for Industrial Mathematics. London (England): London Mathematical Society.
- Fenton, Norman; Neil, Martin E. (July 23, 2004). "Combining evidence in risk analysis using Bayesian Networks" (pdf). Safety Critical Systems Club Newsletter 13 (4) (Newcastle upon Tyne, England): pp. 8–13. https://www.dcs.qmul.ac.uk/~norman/papers/Combining%20evidence%20in%20risk%20analysis%20using%20BNs.pdf.
- Heckerman, David (March 1, 1995). "Tutorial on Learning with Bayesian Networks". In Jordan, Michael Irwin. Learning in Graphical Models. Adaptive Computation and Machine Learning. Cambridge, Massachusetts: MIT Press. 1998. pp. 301–354. ISBN 0-262-60032-3. http://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-95-06..
- Also appears as Heckerman, David (March 1997). "Bayesian Networks for Data Mining". Data Mining and Knowledge Discovery (Netherlands: Springer Netherlands) 1 (1): 79–119. doi:10.1023/A:1009730122752. ISSN 1384-5810.
- An earlier version appears as Technical Report MSR-TR-95-06, Microsoft Research, March 1, 1995. The paper is about both parameter and structure learning in Bayesian networks.
- Jensen, Finn V; Nielsen, Thomas D. (June 6, 2007). Bayesian Networks and Decision Graphs. Information Science and Statistics series (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-68281-5.
- Korb, Kevin B.; Nicholson, Ann E. (September 25, 2003). Bayesian Artificial Intelligence. CRC Computer Science & Data Analysis. Chapman & Hall (CRC Press). doi:10.1007/s10044-004-0214-5. ISBN 1-58488-387-1.
- Neil, Martin; Fenton, Norman E.; Tailor, Manesh (August 2005). Greenberg, Michael R.. ed. "Using Bayesian Networks to Model Expected and Unexpected Operational Losses" (pdf). Risk Analysis: an International Journal (John Wiley & Sons) 25 (4): 963–972. doi:10.1111/j.1539-6924.2005.00641.x. PMID 16268944. http://www.dcs.qmul.ac.uk/~norman/papers/oprisk.pdf.
- Pearl, Judea (September 1986). "Fusion, propagation, and structuring in belief networks". Artificial Intelligence (Elsevier) 29 (3): 241–288. doi:10.1016/0004-3702(86)90072-X. ISSN 0004-3702.
- Pearl, Judea (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Representation and Reasoning Series (2nd printing ed.). San Francisco, California: Morgan Kaufmann. ISBN 0-934613-73-7.
- Pearl, Judea; Russell, Stuart (November 2002). "Bayesian Networks". In Arbib, Michael A.. Handbook of Brain Theory and Neural Networks. Cambridge, Massachusetts: Bradford Books (MIT Press). pp. 157–160. ISBN 0-262-01197-2.
- Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2, http://aima.cs.berkeley.edu/.
- Zhang, Nevin Lianwen; Poole, David (May 1994). "A simple approach to Bayesian network computations". Proceedings of the Tenth Biennial Canadian Artificial Intelligence Conference (AI-94). (Banff, Alberta): 171–178. This paper presents variable elimination for belief networks.
External links
Categories:- Bayesian networks
- Bayesian statistics
- Networks
- Statistical models
- Graphical models
Wikimedia Foundation. 2010.