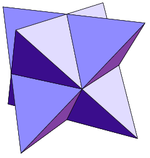
- Octahedral symmetry
-
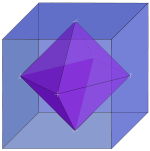
 The cube is the most common shape with octahedral symmetry
The cube is the most common shape with octahedral symmetry
A regular octahedron has 24 rotational (or orientation-preserving) symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the dual of an octahedron.
The group of orientation-preserving symmetries is S4, the symmetric group or the group of permutations of four objects, since there is exactly one such symmetry for each permutation of the four pairs of opposite sides of the octahedron.
Contents
Details
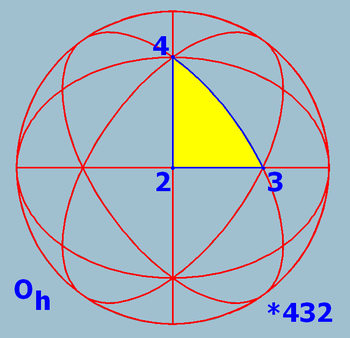
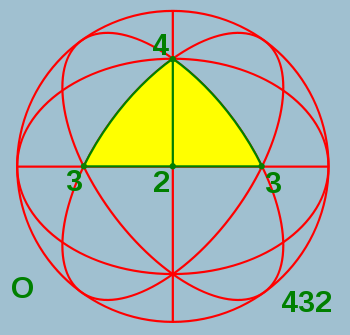 The octahedral rotation group O with fundamental domain
The octahedral rotation group O with fundamental domain
Chiral and full (or achiral) octahedral symmetry are the discrete point symmetries (or equivalently, symmetries on the sphere) with the largest symmetry groups compatible with translational symmetry. They are among the crystallographic point groups of the cubic crystal system.
Chiral octahedral symmetry
O, 432, or [4,3]+ of order 24, is chiral octahedral symmetry or rotational octahedral symmetry . This group is like chiral tetrahedral symmetry T, but the C2 axes are now C4 axes, and additionally there are 6 C2 axes, through the midpoints of the edges of the cube. Td and O are isomorphic as abstract groups: they both correspond to S4, the symmetric group on 4 objects. Td is the union of T and the set obtained by combining each element of O \ T with inversion. O is the rotation group of the cube and the regular octahedron.
Subgroups
- O and T
- D4, D3 and D2
- C4, C3 and C2
- E
Conjugacy classes
- identity
- 6 × rotation by 90°
- 8 × rotation by 120°
- 3 × rotation by 180° about a 4-fold axis
- 6 × rotation by 180° about a 2-fold axis
Achiral octahedral symmetry
- Oh, *432, [4,3]+, or m3m of order 48 - achiral octahedral symmetry or full octahedral symmetry. This group has the same rotation axes as O, but with mirror planes, comprising both the mirror planes of Td and Th. This group is isomorphic to S4 × C2, and is the full symmetry group of the cube and octahedron. It is the hyperoctahedral group for n = 3. See also the isometries of the cube.
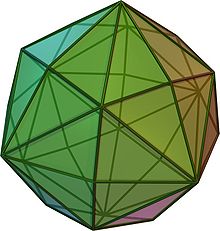 In the disdyakis dodecahedron one full face is a fundamental domain; other solids with the same symmetry can be obtained by adjusting the orientation of the faces, e.g. flattening selected subsets of faces to combine each subset into one face, or replacing each face by multiple faces, or a curved surface.
In the disdyakis dodecahedron one full face is a fundamental domain; other solids with the same symmetry can be obtained by adjusting the orientation of the faces, e.g. flattening selected subsets of faces to combine each subset into one face, or replacing each face by multiple faces, or a curved surface.
With the 4-fold axes as coordinate axes, a fundamental domain of Oh is given by 0 ≤ x ≤ y ≤ z. An object with this symmetry is characterized by the part of the object in the fundamental domain, for example the cube is given by z = 1, and the octahedron by x + y + z = 1 (or the corresponding inequalities, to get the solid instead of the surface). ax + by + cz = 1 gives a polyhedron with 48 faces, e.g. the disdyakis dodecahedron.Faces are 8-by-8 combined to larger faces for a = b = 0 (cube) and 6-by-6 for a = b = c (octahedron).
Subgroups
- Oh
- O, Th, Td and T
- D4h and D2h
- D3d and D2d
- D4, D3 and D2
- C4h, C3h and C2h
- C4v, C3v and C2v
- C4, C3 and C2
- S6, S4 and S2=Ci
- E and Cs
Conjugacy classes
- inversion
- 6 × rotoreflection by 90°
- 8 × rotoreflection by 60°
- 3 × reflection in a plane perpendicular to a 4-fold axis
- 6 × reflection in a plane perpendicular to a 2-fold axis
The isometries of the cube
(To be integrated in the rest of the text.)
The cube has 48 isometries, forming the symmetry group Oh, isomorphic to S4 × C2. They can be categorized as follows:
- O (the identity and 23 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the body diagonals and the unit quaternion representation):
- identity (identity; 1)
- rotation about an axis from the center of a face to the center of the opposite face by an angle of 90°: 3 axes, 2 per axis, together 6 ((1 2 3 4), etc.; ((1±i)/√2, etc.)
- ditto by an angle of 180°: 3 axes, 1 per axis, together 3 ((1 2)(3 4), etc.; i,j,k)
- rotation about an axis from the center of an edge to the center of the opposite edge by an angle of 180°: 6 axes, 1 per axis, together 6 ((1 2), etc.; ((i±j)/√2, etc.)
- rotation about a body diagonal by an angle of 120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; (1±i±j±k)/2)
- The same with inversion (x is mapped to −x) (also 24 isometries). Note that rotation by an angle of 180° about an axis combined with inversion is just reflection in the perpendicular plane. The combination of inversion and rotation about a body diagonal by an angle of 120° is rotation about the body diagonal by an angle of 60°, combined with reflection in the perpendicular plane (the rotation itself does not map the cube to itself; the intersection of the reflection plane with the cube is a regular hexagon).
An isometry of the cube can be identified in various ways:
- by the faces three given adjacent faces (say 1, 2, and 3 on a die) are mapped to
- by the image of a cube with on one face a non-symmetric marking: the face with the marking, whether it is normal or a mirror image, and the orientation
- by a permutation of the four body diagonals (each of the 24 permutations is possible), combined with a toggle for inversion of the cube, or not
For cubes with colors or markings (like dice have), the symmetry group is a subgroup of Oh. Examples:
- C4v: if one face has a different color (or two opposite faces have colors different from each other and from the other four), the cube has 8 isometries, like a square has in 2D.
- D2h: if opposite faces have the same colors, different for each set of two, the cube has 8 isometries, like a cuboid.
- D4h: if two opposite faces have the same color, and all other faces have one different color, the cube has 16 isometries, like a square prism (square box).
- C2v:
- if two adjacent faces have the same color, and all other faces have one different color, the cube has 4 isometries.
- if three faces, of which two opposite to each other, have one color and the other three one other color, the cube has 4 isometries.
- if two opposite faces have the same color, and two other opposite faces also, and the last two have different colors, the cube has 4 isometries, like a piece of blank paper with a shape with a mirror symmetry.
- Cs:
- if two adjacent faces have colors different from each other, and the other four have a third color, the cube has 2 isometries.
- if two opposite faces have the same color, and all other faces have different colors, the cube has 2 isometries, like an asymmetric piece of blank paper.
- C3v: if three faces, of which none opposite to each other, have one color and the other three one other color, the cube has 6 isometries.
For some larger subgroups a cube with that group as symmetry group is not possible with just coloring whole faces. One has to draw some pattern on the faces. Examples:
- D2d: if one face has a line segment dividing the face into two equal rectangles, and the opposite has the same in perpendicular direction, the cube has 8 isometries; there is a symmetry plane and 2-fold rotational symmetry with an axis at an angle of 45° to that plane, and, as a result, there is also another symmetry plane perpendicular to the first, and another axis of 2-fold rotational symmetry perpendicular to the first.
- Th: if each face has a line segment dividing the face into two equal rectangles, such that the line segments of adjacent faces do not meet at the edge, the cube has 24 isometries: the even permutations of the body diagonals and the same combined with inversion (x is mapped to −x).
- Td: if the cube consists of eight smaller cubes, four white and four black, put together alternatingly in all three standard directions, the cube has again 24 isometries: this time the even permutations of the body diagonals and the inverses of the other proper rotations.
- T: if each face has the same pattern with 2-fold rotational symmetry, say the letter S, such that at all edges a top of one S meets a side of the other S, the cube has 12 isometries: the even permutations of the body diagonals.
The full symmetry of the cube (Oh) is preserved if and only if all faces have the same pattern such that the full symmetry of the square is preserved, with for the square a symmetry group of order 8.
The full symmetry of the cube under proper rotations (O) is preserved if and only if all faces have the same pattern with 4-fold rotational symmetry.
Octahedral symmetry of the Bolza surface
In Riemann surface theory, the Bolza surface, sometimes called the Bolza curve, is obtained as the ramified double cover of the Riemann sphere, with ramification locus at the set of vertices of the regular inscribed octahedron. Its automorphism group includes the hyperelliptic involution which flips the two sheets of the cover. The quotient by the order 2 subgroup generated by the hyperelliptic involution yields precisely the group of symmetries of the octahedron. Among the many remarkable properties of the Bolza surface is the fact that it maximizes the systole among all genus 2 hyperbolic surfaces.
Chiral solids with octahedral rotational symmetry
- Note to Pentagonal icositetrahedron: (Ccw) - note that, not very clear in the image, at some vertices 4 faces meet (in the edge of the image)
Archimedean solids
Name picture Faces Edges Vertices Vertex configuration snub cube
or snub cuboctahedron (2 chiral forms)
(Video)
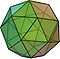
(Video)38 32 triangles
6 squares60 24 3,3,3,3,4 Catalan solids
Name picture Dual Archimedean solid Faces Edges Vertices Face Polygon pentagonal icositetrahedron 

(Video)(Video)snub cube 24 60 38 irregular pentagon Solids with full octahedral symmetry
Platonic solids
Name Picture Faces Edges Vertices Edges per face Faces meeting
at each vertexcube (hexahedron) 
(Animation)
6 12 8 4 3 octahedron 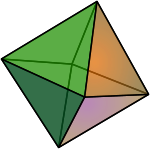
(Animation)8 12 6 3 4 Archimedean solids
(semi-regular: vertex-uniform)
Name picture Faces Edges Vertices Vertex configuration cuboctahedron
(quasi-regular: vertex- and edge-uniform)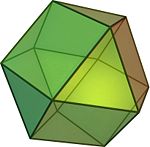
(Video)14 8 triangles
6 squares24 12 3,4,3,4 truncated cube
or truncated hexahedron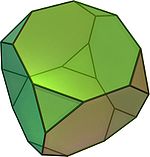
(Video)14 8 triangles
6 octagons36 24 3,8,8 truncated octahedron 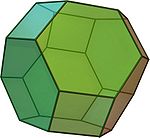
(Video)14 6 squares
8 hexagons36 24 4,6,6 rhombicuboctahedron
or small rhombicuboctahedron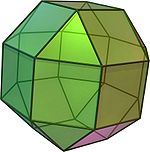
(Video)26 8 triangles
18 squares48 24 3,4,4,4 truncated cuboctahedron
or great rhombicuboctahedron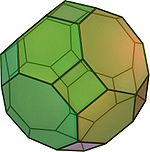
(Video)26 12 squares
8 hexagons
6 octagons72 48 4,6,8 Catalan solids
(semi-regular duals: face-uniform)
Name picture Dual Archimedean solid Faces Edges Vertices Face polygon rhombic dodecahedron
(quasi-regular dual: face- and edge-uniform)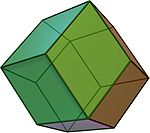
(Video)cuboctahedron 12 24 14 rhombus triakis octahedron 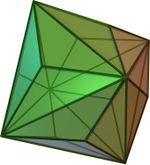
(Video)truncated cube 24 36 14 isosceles triangle tetrakis hexahedron 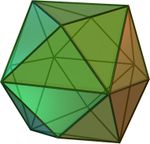
(Video)truncated octahedron 24 36 14 isosceles triangle deltoidal icositetrahedron 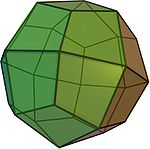
(Video)rhombicuboctahedron 24 48 26 kite disdyakis dodecahedron
or hexakis octahedron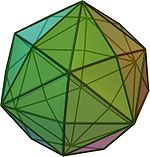
(Video)truncated cuboctahedron 48 72 26 scalene triangle Other
See also
- tetrahedral symmetry
- icosahedral symmetry
- binary octahedral group
- hyperoctahedral group
Categories:- Finite groups
- Rotational symmetry
Wikimedia Foundation. 2010.