- Continuity equation
-
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.
Continuity equations are the (stronger) local form of conservation laws. All the examples of continuity equations below express the same idea, which is roughly that: the total amount (of the conserved quantity) inside any region can only change by the amount that passes in or out of the region through the boundary. A conserved quantity cannot increase or decrease, it can only move from place to place.
Any continuity equation can be expressed in an "integral form" (in terms of a flux integral), which applies to any finite region, or in a "differential form" (in terms of the divergence operator) which applies at a point. In this article, only the "differential form" versions will be given; see the article divergence theorem for how to express any of these laws in "integral form".
Contents
General equation
Differential form
The differential form for a general continuity equation is
where
- φ is some quantity per unit volume,
- f is a vector function describing the flux (flow per unit area and unit time) of
 ,
, - ∇∙ is divergence,
- t is time,
- and s is the generation (negative in the case of removal) per unit volume and unit time of φ. Terms that generate (s > 0) or remove (s < 0) φ are referred to as a "sources" and "sinks" respectively.
In the case that φ is a conserved quantity that cannot be created or destroyed (such as energy density), the continuity equation is:
because s = 0.
This general equation may be used to derive any continuity equation, ranging from as simple as the volume continuity equation to as complicated as the Navier–Stokes equations. This equation also generalizes the advection equation.
Note the flux f should represent some flow or transport, which has dimensions [quantity][T]-1[L]-2, where [quantity]/[L]3 is the dimension of φ.
Other equations in physics, such as Gauss's law of the electric field and Gauss's law for gravity, have a similar mathematical form to the continuity equation, but are not usually called by the term "continuity equation", because f in those cases does not represent the flow of a real physical quantity.
Integral form
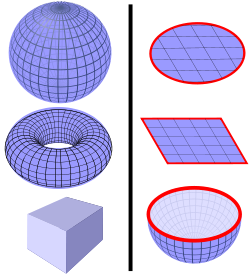 In the integral form of the continuity equation, S is any imaginary closed surface that fully encloses a volume V, like any of the surfaces on the left. S can not be a surface with boundaries that do not enclose a volume, like those on the right. (Surfaces are blue, boundaries are red.)
In the integral form of the continuity equation, S is any imaginary closed surface that fully encloses a volume V, like any of the surfaces on the left. S can not be a surface with boundaries that do not enclose a volume, like those on the right. (Surfaces are blue, boundaries are red.)
By the divergence theorem (see below), the continuity equation can be rewritten in an equivalent way, called the "integral form":
where
- S is a closed surface that encloses a volume V. S is arbitrary but fixed (unchanging in time) for the calculation;
 denotes a volume integral over V. The notation
denotes a volume integral over V. The notation  is used here since V must be closed (
is used here since V must be closed ( is sufficient but emphasises a closed volume less);
is sufficient but emphasises a closed volume less); denotes a surface integral,
denotes a surface integral,  is the outward-pointing unit normal to the surface S;
is the outward-pointing unit normal to the surface S; are equivalent notatations for the surface integral, becuase
are equivalent notatations for the surface integral, becuase  ;
; is the total amount of φ in the volume V (for example, if φ is the mass density, then q is the total mass in the volume V);
is the total amount of φ in the volume V (for example, if φ is the mass density, then q is the total mass in the volume V); is the total generation (negative in the case of removal) per unit time by the sources and sinks in the volume V;
is the total generation (negative in the case of removal) per unit time by the sources and sinks in the volume V;
In a simple example, V could be a building, and q could be the number of people in the building. The surface S would consist of the walls, doors, roof, and foundation of the building. Then the continuity equation states that the number of people in the building increases when people enter the building (an inward flux through the surface), decreases when people exit the building (an outward flux through the surface), increases when someone in the building gives birth (a "source" where s > 0), and decreases when someone in the building dies (a "sink" where s < 0).
Proof of equivalence
Starting from the differential form:
which is for unit volume, multiplying throughout by the infinitesimal volume element dV and integrating over the region gives the total amounts quantities in the volume of the region (per unit time):
V is constant in shape for the calculation, so it is independent of time and the time derivatives can be freely moved out of the first integral on the left side,
where ordinary derivatives replace partial derivatives since the integral becomes a function of time only (the integral is evaluated over the region - so the spatial variables become removed from the final expression and time remains the only variable). Now using the divergence theorem for the second integral on the left side:
The right side becomes:
Substituting these in obtains the integral form:
Electromagnetic theory
Main article: Charge conservation3-currents
In electromagnetic theory, the continuity equation can either be regarded as an empirical law expressing (local) charge conservation, or can be derived as a consequence of two of Maxwell's equations. It states that the divergence of the current density J (in amperes per square meter) is equal to the negative rate of change of the charge density ρ (in coulombs per cubic metre),

Derivation from Maxwell's equations
One of Maxwell's equations, Ampère's law (with Maxwell's correction), states that
Taking the divergence of both sides results in
but the divergence of a curl is zero, so that
Another one of Maxwell's equations, Gauss's law, states that
Substitute this into equation (1) to obtain
which is the continuity equation.
4-currents
Conservation of a current (not necessarily an electromagnetic current) is expressed compactly as the Lorentz invariant divergence of a four-current:
where
- c is the speed of light
- ρ; the charge density
- j the conventional 3-current density.
- μ; labels the space-time dimension
so that since
then
implies that the current is conserved:
Interpretation
Current is the movement of charge. The continuity equation says that if charge is moving out of a differential volume (i.e. divergence of current density is positive) then the amount of charge within that volume is going to decrease, so the rate of change of charge density is negative. Therefore the continuity equation amounts to a conservation of charge.
Fluid dynamics
In fluid dynamics, the continuity equation states that, in any steady state process, the rate at which mass enters a system is equal to the rate at which mass leaves the system.[1][2] In fluid dynamics, the continuity equation is analogous to Kirchhoff's current law in electric circuits.
The differential form of the continuity equation is:[1]

where
- ρ is fluid density,
- t is time,
- u is the flow velocity vector field.
If density (ρ) is a constant, as in the case of incompressible flow, the mass continuity equation simplifies to a volume continuity equation:[1]
which means that the divergence of velocity field is zero everywhere. Physically, this is equivalent to saying that the local volume dilation rate is zero.
Further, the Navier-Stokes equations form a vector continuity equation describing the conservation of linear momentum.
Derivation from first principles
Suppose an amount of mass M is contained in a region of volume V. This is equal to:
the rate of change of mass leaving the region is simply the time derivative:
where the minus sign has been inserted since the mass is decreasing in the region. Partial derivatives are used since they enter the integrand, which is not only a function of time, but space due to the density function. The rate of change of mass crossing the boundary and leaving the region is also equal to
by the divergence theorem:
Equating these expressions leads to an identity of volume integrals,
hence the integrands must be equal, which directly leads to the continuity equation:
Energy
By conservation of energy, which can only be transferred and not created or destroyed leads to a continuity equation, an alternative mathematical statement of energy conservation to the thermodynamic laws.
Letting
- u = local energy density (energy per unit volume),
- q = energy flux (transfer of energy per unit cross-sectional area per unit time) as a vector,
the continuity equation is:

Thermodynamics
By Fourier's law for a uniformly conducting medium,

where k is the thermal conductivity (not Boltzmann constant), this can also be written as:


Quantum mechanics
In quantum mechanics, the conservation of probability also yields a continuity equation. The terms in the equation require these definitions, and are slightly less obvious than the other forms of volume densities, currents, current densities etc., so they are outlined here:
- The wavefunction Ψ for a single particle in the position-time space (rather than momentum space) - i.e. functions of position r and time t, Ψ = Ψ(r, t) = (x, y, z, t).
- The probability density function ρ = ρ(r, t) is:
- The probability that a measurement of the particle's position will yield a value within V at t, denoted by P = Pr ∈ V(t), is:
- The probability current (aka probability flux) j:
With these definitions the continuity equation reads:

Either form is usually quoted. Intuitively; considering the above quantities this represents the flow of probability. The chance of finding the particle at some r t flows like a fluid, the particle itself does not flow deterministically in the same vector field.
Derivation from Schrödinger's equation
For this derivation see for example [3]. The 3-d time dependant Schrödinger equation and its complex conjugate (i → –i) throughout are respectively:
where U is the potential function. The partial derivative of ρ with respect to t is:
Multiplying the Schrödinger equation by Ψ*, and similarly multiplying the complex conjugated Schrödinger equation by Ψ, then solving for time partial derivative terms:
Substituting these into the time derivative of ρ:
The Laplacian operators (∇2) in the above result suggest that the right hand side is the divergence of j, and the reversed order of terms imply this is the negative of j, altogether:
so the continuity equation is:
The intgeral form follows as for the general equation.
Derivation from the wavefunction probability distribution
The time derivative of P is
where the last equality follows from the product rule and the fact that the shape of V is fixed for the calculation and therefore independent of time - i.e. the time derivative can be moved through the integral. To simplify this further consider again the time dependent Schrödinger equation and its complex conjugate, in terms of the time derivatives of Ψ and Ψ* respectively:
Substituting into the preceding equation:
 .
.
From the product rule for the divergence operator
substituting:
In the expression for P, the argument of the divergence operator is j,
using the divergence theorem again gives the integral form:
To obtain the differential form:
The differential form follows from the fact that the preceding equation holds for all V, and as the integrand is a continuous function of space, it must vanish everywhere:
See also
- Conservation law
- Euler equations
- Groundwater energy balance
- Incompressible fluid
- Mass flow rate
- Noether's Theorem
- Probability density function
- Schrödinger equation
Notes
Categories:- Equations of fluid dynamics
- Conservation equations
- Partial differential equations
-
Wikimedia Foundation. 2010.


























![\mathbf{j} = \frac{\hbar}{2mi} \left [ \Psi^{*} \left ( \nabla \Psi \right ) - \Psi \left ( \nabla \Psi^{*} \right ) \right ].](e/bde9dc92855b78f5ee62f50445a5bd6e.png)


![\begin{align} & \Psi^{*}\frac{\partial \Psi}{\partial t} = \frac{1}{i\hbar } \left [ -\frac{\hbar^2\Psi^{*}}{2m}\nabla^2 \Psi + U\Psi^{*}\Psi \right ], \\
& \Psi \frac{\partial \Psi^{*}}{\partial t} = - \frac{1}{i\hbar } \left [ - \frac{\hbar^2\Psi}{2m}\nabla^2 \Psi^{*} + U\Psi\Psi^{*} \right ].\\
\end{align}](5/84599e4eb49592809679c354b1b104b6.png)
![\begin{align}
\frac{\partial \rho}{\partial t} & = \frac{1}{i\hbar } \left [ -\frac{\hbar^2\Psi^{*}}{2m}\nabla^2 \Psi + U\Psi^{*}\Psi \right ] - \frac{1}{i\hbar } \left [ - \frac{\hbar^2\Psi}{2m}\nabla^2 \Psi^{*} + U\Psi\Psi^{*} \right ] \\
& = \frac{\hbar}{2im} \left [ \Psi\nabla^2 \Psi^{*} - \Psi^{*}\nabla^2 \Psi \right ] \\
\end{align}](9/d894d413e02f8d0137b62fb4990e646e.png)
![\begin{align} \nabla \cdot \mathbf{j} & = \nabla \cdot \left [ \frac{\hbar}{2mi} \left ( \Psi^{*} \left ( \nabla \Psi \right ) - \Psi \left ( \nabla \Psi^{*} \right ) \right ) \right ] \\
& = \frac{\hbar}{2mi} \left [ \Psi^{*} \left ( \nabla^2 \Psi \right ) - \Psi \left ( \nabla^2 \Psi^{*} \right ) \right ] \\
& = - \frac{\hbar}{2mi} \left [ \Psi \left ( \nabla^2 \Psi^{*} \right ) - \Psi^{*} \left ( \nabla^2 \Psi \right ) \right ] \\
\end{align}](5/8159dc7c7c95f21b7f577568b00bd1d4.png)


![\begin{align} & \frac{\partial \Psi}{\partial t} = \frac{i \hbar}{2m} \nabla^2 \Psi - \frac{i}{\hbar} U \Psi \\
& \frac{\partial \Psi^*}{\partial t} = - \left [ \frac{i \hbar}{2m} \nabla^2 \Psi* - \frac{i}{\hbar} U \Psi* \right ] \\
\end{align}\,\!](4/3047716331aa2004bfd4f4ce2f7a93df.png)

![\oint_V \frac{\partial |\Psi|^2}{\partial t} \mathrm{d}V = - \oint_V \nabla \cdot \left [ \frac{\hbar}{2mi} \left(\Psi^* \nabla \Psi - \Psi \nabla \Psi^* \right ) \right ] \mathrm{d}V](9/e69214fab5276f0390b80c752dd778f1.png)



