- Gravitational constant
-
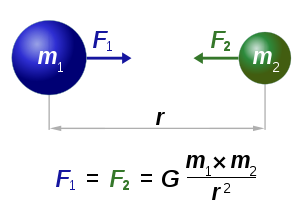 The gravitational constant G is a key quantity in Newton's law of universal gravitation.
The gravitational constant G is a key quantity in Newton's law of universal gravitation.
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal gravitational constant, Newton's constant, and colloquially Big G.[1] It should not be confused with "little g" (g), which is the local gravitational field (equivalent to the free-fall acceleration[2]), especially that at the Earth's surface; see Gravity of Earth and Standard gravity.
According to the law of universal gravitation, the attractive force (F) between two bodies is proportional to the product of their masses (m1 and m2), and inversely proportional to the square of the distance (r) between them:
The constant of proportionality, G, is the gravitational constant.
The gravitational constant is perhaps the most difficult physical constant to measure to high accuracy.[3] In SI units, the 2010 CODATA-recommended value of the gravitational constant (with standard uncertainty in parentheses) is:[4]
with relative standard uncertainty 1.2×10−4,[4] or 1 part in 8300.
Contents
Dimensions, units and magnitude
The dimensions assigned to the gravitational constant in the equation above—length cubed, divided by mass and by time squared (in SI units, metres cubed per kilogram per second squared)—are those needed to balance the units of measurements in gravitational equations. However, these dimensions have fundamental significance in terms of Planck units: when expressed in SI units, the gravitational constant is dimensionally and numerically equal to the cube of the Planck length divided by the Planck mass and by the square of Planck time.
In natural units, of which Planck units are perhaps the best example, G and other physical constants such as c (the speed of light) may be set equal to 1.
In many secondary school texts, the dimensions of G are derived from force in order to assist student comprehension:
In cgs, G can be written as:
G can also be given as:
Given the fact that the period P of an object in circular orbit around a spherical object obeys
- GM = 3πV / P2
where V is the volume inside the radius of the orbit, we see that
This way of expressing G shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface.
In some fields of astrophysics where distances are measured in parsecs (pc), velocities in kilometers per second (km/s) and masses in solar units (
 ), it is useful to express G as:
), it is useful to express G as:The gravitational force is extremely weak compared with other fundamental forces. For example, the gravitational force between an electron and proton 1 meter apart is approximately 10−67 newtons, while the electromagnetic force between the same two particles is approximately 10−28 newtons. Both these forces are weak when compared with the forces we are able to experience directly, but the electromagnetic force in this example is some 39 orders of magnitude (i.e., 1039) greater than the force of gravity — roughly the same ratio as the mass of the Sun compared to a microgram mass.
History of measurement
The gravitational constant appears in Newton's law of universal gravitation, but it was not measured until 71 years after Newton's death by Henry Cavendish with his Cavendish experiment, performed in 1798 (Philosophical Transactions 1798). Cavendish measured G implicitly, using a torsion balance invented by the geologist Rev. John Michell. He used a horizontal torsion beam with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam's oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. Cavendish's aim was not actually to measure the gravitational constant, but rather to measure the Earth's density relative to water, through the precise knowledge of the gravitational interaction. In retrospect, the density that Cavendish calculated implies a value for G of 6.754 × 10−11 m3/kg/s2.[5]
The accuracy of the measured value of G has increased only modestly since the original Cavendish experiment. G is quite difficult to measure, as gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies. Furthermore, gravity has no established relation to other fundamental forces, so it does not appear possible to calculate it indirectly from other constants that can be measured more accurately, as is done in some other areas of physics. Published values of G have varied rather broadly, and some recent measurements of high precision are, in fact, mutually exclusive.[3][6]
In the January 5, 2007 issue of Science (page 74), the report "Atom Interferometer Measurement of the Newtonian Constant of Gravity" (J. B. Fixler, G. T. Foster, J. M. McGuirk, and M. A. Kasevich) describes a new measurement of the gravitational constant. According to the abstract: "Here, we report a value of G = 6.693 × 10−11 cubic meters per kilogram second squared, with a standard error of the mean of ±0.027 × 10−11 and a systematic error of ±0.021 × 10−11 cubic meters per kilogram second squared."[7]
The GM product
Main article: Standard gravitational parameterThe quantity GM—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or the Earth—is known as the standard gravitational parameter and is denoted
 . Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names.
. Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names.This quantity gives a convenient simplification of various gravity-related formulas. Also, for celestial bodies such as the Earth and the Sun, the value of the product GM is known more accurately than each factor independently. Indeed, the limited accuracy available for G often limits the accuracy of scientific determination of such masses in the first place.
For Earth, using M⊕ as the symbol for the mass of the Earth, we have
Calculations in celestial mechanics can also be carried out using the unit of solar mass rather than the standard SI unit kilogram. In this case we use the Gaussian gravitational constant which is k2, where
and
 is the astronomical unit;
is the astronomical unit; is the mean solar day;
is the mean solar day; is the solar mass.
is the solar mass.
If instead of mean solar day we use the sidereal year as our time unit, the value of ks is very close to 2π (k = 6.28315).
The standard gravitational parameter GM appears as above in Newton's law of universal gravitation, as well as in formulas for the deflection of light caused by gravitational lensing, in Kepler's laws of planetary motion, and in the formula for escape velocity.
See also
Notes
- ^ "University of Washington Big G Measurement". Astrophysics Science Division. Goddard Space Flight Center. 2002-12-23. http://asd.gsfc.nasa.gov/Stephen.Merkowitz/G/Big_G.html. "Since Cavendish first measured Newton's Gravitational constant 200 years ago, "Big G" remains one of the most elusive constants in physics."
- ^ Fundamentals of Physics 8ed,Halliday/Resnick/Walker,ISBN 978-0-470-04618-0 p 336
- ^ a b George T. Gillies (1997), "The Newtonian gravitational constant: recent measurements and related studies", Reports on Progress in Physics 60 (2): 151–225, Bibcode 1997RPPh...60..151G, doi:10.1088/0034-4885/60/2/001, http://www.iop.org/EJ/abstract/0034-4885/60/2/001. A lengthy, detailed review. See Figure 1 and Table 2 in particular.
- ^ a b P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants [Thursday, 02-Jun-2011 21:00:12 EDT]. National Institute of Standards and Technology, Gaithersburg, MD 20899.
- ^ Brush, Stephen G.; Holton, Gerald James (2001), Physics, the human adventure: from Copernicus to Einstein and beyond, New Brunswick, N.J: Rutgers University Press, pp. 137, ISBN 0-8135-2908-5
- ^ Peter J. Mohr; Barry N. Taylor (January 2005), "CODATA recommended values of the fundamental physical constants: 2002" (PDF), Reviews of Modern Physics 77 (1): 1–107, Bibcode 2005RvMP...77....1M, doi:10.1103/RevModPhys.77.1, http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other%20rmp%20articles/CODATA2005.pdf, retrieved 2006-07-01. Section Q (pp. 42–47) describes the mutually inconsistent measurement experiments from which the CODATA value for G was derived.
- ^ J. B. Fixler; G. T. Foster; J. M. McGuirk; M. A. Kasevich (2007-01-05), "Atom Interferometer Measurement of the Newtonian Constant of Gravity", Science 315 (5808): 74–77, Bibcode 2007Sci...315...74F, doi:10.1126/science.1135459, PMID 17204644, http://www.sciencemag.org/cgi/content/abstract/315/5808/74
References
- E. Myles Standish. "Report of the IAU WGAS Sub-group on Numerical Standards". In Highlights of Astronomy, I. Appenzeller, ed. Dordrecht: Kluwer Academic Publishers, 1995. (Complete report available online: PostScript; PDF. Tables from the report also available: Astrodynamic Constants and Parameters)
- Jens H. Gundlach; Stephen M. Merkowitz (2000), "Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback", Physical Review Letters 85 (14): 2869–2872, arXiv:gr-qc/0006043, Bibcode 2000PhRvL..85.2869G, doi:10.1103/PhysRevLett.85.2869, PMID 11005956
External links
- Newtonian constant of gravitation G at the National Institute of Standards and Technology References on Constants, Units, and Uncertainty
- The Controversy over Newton's Gravitational Constant — additional commentary on measurement problems
- The Gravitational Constant
Categories:- Celestial mechanics
- Gravitation
- Fundamental constants
Wikimedia Foundation. 2010.









