- Circle
-
This article is about the shape and mathematical concept. For other uses, see Circle (disambiguation).
 Tycho crater, one of many examples of circles that arise in nature.
Tycho crater, one of many examples of circles that arise in nature.
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.
Circles are simple closed curves which divide the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and the latter is called a disk.
A circle is a special ellipse in which the two foci are coincident and the eccentricity is 0. Circles are conic sections attained when a right circular cone is intersected by a plane perpendicular to the axis of the cone.
A circle can also be defined as the curve traced out by a point that moves so that its distance from a given point is constant.
Contents
Terminology
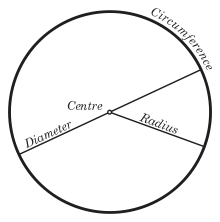
A circle's diameter is the length of a line segment whose endpoints lie on the circle and which passes through the centre. This is the largest distance between any two points on the circle. The diameter of a circle is twice the radius, or distance from the centre to the circle's boundary. The terms "diameter" and "radius" also refer to the line segments which fit these descriptions. The circumference is the distance around the outside of a circle.
A chord is a line segment whose endpoints lie on the circle. A diameter is the longest chord in a circle. A tangent to a circle is a straight line that touches the circle at a single point, while a secant is an extended chord: a straight line cutting the circle at two points.
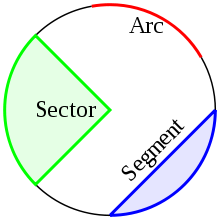
An arc of a circle is any connected part of the circle's circumference. A sector is a region bounded by two radii and an arc lying between the radii, and a segment is a region bounded by a chord and an arc lying between the chord's endpoints.
History
The word "circle" derives from the Greek, kirkos "a circle," from the base ker- which means to turn or bend. The origins of the words "circus" and "circuit" are closely related.
The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern civilization possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy, and calculus.
Early science, particularly geometry and astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles.[citation needed]
Some highlights in the history of the circle are:
- 1700 BC – The Rhind papyrus gives a method to find the area of a circular field. The result corresponds to 256/81 (3.16049...) as an approximate value of π.[1]
- 300 BC – Book 3 of Euclid's Elements deals with the properties of circles.
- In Plato's Seventh Letter there is a detailed definition and explanation of the circle. Plato explains the perfect circle, and how it is different from any drawing, words, definition or explanation.
- 1880 – Lindemann proves that π is transcendental, effectively settling the millennia-old problem of squaring the circle.[2]
Analytic results
Length of circumference
Further information: PiThe ratio of a circle's circumference to its diameter is π (pi), an irrational constant approximately equal to 3.141592654. Thus the length of the circumference C is related to the radius r and diameter d by:
Area enclosed
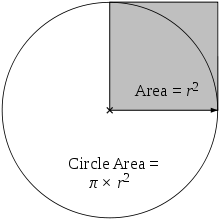
Main article: Area of a diskAs proved by Archimedes, the area enclosed by a circle is equal to that of a triangle whose base has the length of the circle's circumference and whose height equals the circle's radius,[3] which comes to π multiplied by the radius squared:
Equivalently, denoting diameter by d,
that is, approximately 79 percent of the circumscribing square (whose side is of length d).
The circle is the plane curve enclosing the maximum area for a given arc length. This relates the circle to a problem in the calculus of variations, namely the isoperimetric inequality.
Equations
Cartesian coordinates
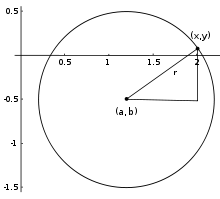
In an x-y Cartesian coordinate system, the circle with centre coordinates (a, b) and radius r is the set of all points (x, y) such that
This equation of the circle follows from the Pythagorean theorem applied to any point on the circle: as shown in the diagram to the right, the radius is the hypotenuse of a right-angled triangle whose other sides are of length x − a and y − b. If the circle is centred at the origin (0, 0), then the equation simplifies to
The equation can be written in parametric form using the trigonometric functions sine and cosine as
where t is a parametric variable in the range 0 to 2π, interpreted geometrically as the angle that the ray from (a, b) to (x, y) makes with the x-axis. An alternative parametrisation of the circle is:
In this parametrisation, the ratio of t to r can be interpreted geometrically as the stereographic projection of the circle onto the line passing through the centre parallel to the x-axis.
In homogeneous coordinates each conic section with equation of a circle is of the form
It can be proven that a conic section is a circle exactly when it contains (when extended to the complex projective plane) the points I(1: i: 0) and J(1: −i: 0). These points are called the circular points at infinity.
Polar coordinates
In polar coordinates the equation of a circle is:
where a is the radius of the circle, r0 is the distance from the origin to the centre of the circle, and φ is the anticlockwise angle from the positive x-axis to the line connecting the origin to the centre of the circle. For a circle centred at the origin, i.e. r0 = 0, this reduces to simply r = a. When r0 = a, or when the origin lies on the circle, the equation becomes
In the general case, the equation can be solved for r, giving
 ,
,
the solution with a minus sign in front of the square root giving the same curve.
Complex plane
In the complex plane, a circle with a centre at c and radius (r) has the equation
 . In parametric form this can be written z = reit + c.
. In parametric form this can be written z = reit + c.The slightly generalised equation
 for real p, q and complex g is sometimes called a generalised circle. This becomes the above equation for a circle with
for real p, q and complex g is sometimes called a generalised circle. This becomes the above equation for a circle with  , since
, since  . Not all generalised circles are actually circles: a generalised circle is either a (true) circle or a line.
. Not all generalised circles are actually circles: a generalised circle is either a (true) circle or a line.Tangent lines
Main article: Tangent lines to circlesThe tangent line through a point P on the circle is perpendicular to the diameter passing through P. If P = (x1, y1) and the circle has centre (a, b) and radius r, then the tangent line is perpendicular to the line from (a, b) to (x1,y1), so it has the form (x1−a)x+(y1−b)y = c. Evaluating at (x1, y1) determines the value of c and the result is that the equation of the tangent is
- (x1 − a)x + (y1 − b)y = (x1 − a)x1 + (y1 − b)y1
or
- (x1 − a)(x − a) + (y1 − b)(y − b) = r2.
If y1≠b then slope of this line is
 .
.
This can also be found using implicit differentiation.
When the centre of the circle is at the origin then the equation of the tangent line becomes
- x1x + y1y = r2,
and its slope is
 .
.
Properties
- The circle is the shape with the largest area for a given length of perimeter. (See Isoperimetric inequality.)
- The circle is a highly symmetric shape: every line through the centre forms a line of reflection symmetry and it has rotational symmetry around the centre for every angle. Its symmetry group is the orthogonal group O(2,R). The group of rotations alone is the circle group T.
- All circles are similar.
- A circle's circumference and radius are proportional.
- The area enclosed and the square of its radius are proportional.
- The constants of proportionality are 2π and π, respectively.
- The circle which is centred at the origin with radius 1 is called the unit circle.
- Thought of as a great circle of the unit sphere, it becomes the Riemannian circle.
- Through any three points, not all on the same line, there lies a unique circle. In Cartesian coordinates, it is possible to give explicit formulae for the coordinates of the centre of the circle and the radius in terms of the coordinates of the three given points. See circumcircle.
Chord
- Chords are equidistant from the centre of a circle if and only if they are equal in length.
- The perpendicular bisector of a chord passes through the centre of a circle; equivalent statements stemming from the uniqueness of the perpendicular bisector:
- A perpendicular line from the centre of a circle bisects the chord.
- The line segment (circular segment) through the centre bisecting a chord is perpendicular to the chord.
- If a central angle and an inscribed angle of a circle are subtended by the same chord and on the same side of the chord, then the central angle is twice the inscribed angle.
- If two angles are inscribed on the same chord and on the same side of the chord, then they are equal.
- If two angles are inscribed on the same chord and on opposite sides of the chord, then they are supplemental.
- For a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.
- An inscribed angle subtended by a diameter is a right angle (see Thales' theorem).
- The diameter is the longest chord of the circle.
- If the intersection of any two chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then ab = cd.
- If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a2 + b2 + c2 + d2 equals the square of the diameter.
- The distance from a point on the circle to a given chord times the diameter of the circle equals the product of the distances from the point to the ends of the chord.[4]:p.71
Sagitta
- The sagitta (also known as the versine) is a line segment drawn perpendicular to a chord, between the midpoint of that chord and the arc of the circle.
- Given the length y of a chord, and the length x of the sagitta, the Pythagorean theorem can be used to calculate the radius of the unique circle which will fit around the two lines:
Another proof of this result which relies only on two chord properties given above is as follows. Given a chord of length y and with sagitta of length x, since the sagitta intersects the midpoint of the chord, we know it is part of a diameter of the circle. Since the diameter is twice the radius, the “missing” part of the diameter is (2r − x) in length. Using the fact that one part of one chord times the other part is equal to the same product taken along a chord intersecting the first chord, we find that (2r − x)x = (y/2)2. Solving for r, we find the required result.
Tangent
- The line perpendicular drawn to a radius through the end point of the radius is a tangent to the circle.
- A line drawn perpendicular to a tangent through the point of contact with a circle passes through the centre of the circle.
- Two tangents can always be drawn to a circle from any point outside the circle, and these tangents are equal in length.
- If a tangent at A and a tangent at B intersect at the exterior point P, then denoting the centre as O, the angles ∠BOA and ∠BPA are supplementary.
- If AD is tangent to the circle at A and if AQ is a chord of the circle, then ∠DAQ =
 arc(AQ).
arc(AQ).
Theorems
See also: Power of a point- The chord theorem states that if two chords, CD and EB, intersect at A, then CA×DA = EA×BA.
- If a tangent from an external point D meets the circle at C and a secant from the external point D meets the circle at G and E respectively, then DC2 = DG×DE. (Tangent-secant theorem.)
- If two secants, DG and DE, also cut the circle at H and F respectively, then DH×DG = DF×DE. (Corollary of the tangent-secant theorem.)
- The angle between a tangent and chord is equal to one half the subtended angle on the opposite side of the chord (Tangent Chord Angle).
- If the angle subtended by the chord at the centre is 90 degrees then l = √2 × r, where l is the length of the chord and r is the radius of the circle.
- If two secants are inscribed in the circle as shown at right, then the measurement of angle A is equal to one half the difference of the measurements of the enclosed arcs (DE and BC). This is the secant-secant theorem.
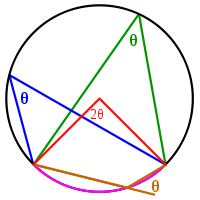
Inscribed angles
See also: Inscribed angle theoremAn inscribed angle (examples are the blue and green angles in the figure) is exactly half the corresponding central angle (red). Hence, all inscribed angles that subtend the same arc (pink) are equal. Angles inscribed on the arc (brown) are supplementary. In particular, every inscribed angle that subtends a diameter is a right angle (since the central angle is 180 degrees).
Circle of Apollonius
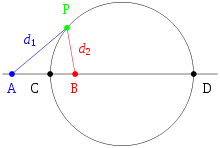
Apollonius of Perga showed that a circle may also be defined as the set of points in a plane having a constant ratio (other than 1) of distances to two fixed foci, A and B.[5][6] (The set of points where the distances are equal is the perpendicular bisector of A and B, a line.) That circle is sometimes said to be drawn about two points.
The proof is in two parts. First, one must prove that, given two foci A and B and a ratio of distances, any point P satisfying the ratio of distances must fall on a particular circle. Let C be another point, also satisfying the ratio and lying on segment AB. By the angle bisector theorem the line segment PC will bisect the interior angle APB, since the segments are similar:
Analogously, a line segment PD through some point D on AB extended bisects the corresponding exterior angle BPQ where Q is on AP extended. Since the interior and exterior angles sum to 180 degrees, the angle CPD is exactly 90 degrees, i.e., a right angle. The set of points P such that angle CPD is a right angle forms a circle, of which CD is a diameter.
Second, see[7]:p.15 for a proof that every point on the indicated circle satisfies the given ratio.
Cross-ratios
A closely related property of circles involves the geometry of the cross-ratio of points in the complex plane. If A, B, and C are as above, then the circle of Apollonius for these three points is the collection of points P for which the absolute value of the cross-ratio is equal to one:
Stated another way, P is a point on the circle of Apollonius if and only if the cross-ratio [A,B;C,P] is on the unit circle in the complex plane.
Generalized circles
See also: Generalized circleIf C is the midpoint of the segment AB, then the collection of points P satisfying the Apollonius condition
 (1)
(1)
is not a circle, but rather a line.
Thus, if A, B, and C are given distinct points in the plane, then the locus of points P satisfying (1) is called a generalized circle. It may either be a true circle or a line. In this sense a line is a generalized circle of infinite radius.
Circles inscribed in or circumscribed about other figures
In every triangle a unique circle, called the incircle, can be inscribed such that it is tangent to each of the three sides of the triangle.
About every triangle a unique circle, called the circumcircle, can be circumscribed such that it goes through each of the triangle's three vertices.
A tangential polygon, such as a tangential quadrilateral, is any convex polygon within which a circle can be inscribed that is tangent to each side of the polygon.
A cyclic polygon is any convex polygon about which a circle can be circumscribed, passing through each vertex. A well-studied example is the cyclic quadrilateral.
A hypocycloid is a curve that is inscribed in a given circle by tracing a fixed point on a smaller circle that rolls within and tangent to the given circle.
Circle as limiting case of other figures
The circle can be viewed as a limiting case of each of various other figures:
- A Cartesian oval is a set of points such that a weighted sum of the distances from any of its points to two fixed points (foci) is a constant. An ellipse is the case in which the weights are equal. A circle is an ellipse with an eccentricity of zero, meaning that the two foci coincide with each other as the centre of the circle. A circle is also a different special case of a Cartesian oval in which one of the weights is zero.
- A superellipse has an equation of the form
 for positive a, b, and n. A supercircle has b=a. A circle is the special case of a supercircle in which n=2.
for positive a, b, and n. A supercircle has b=a. A circle is the special case of a supercircle in which n=2.
- A Cassini oval is a set of points such that the product of the distances from any of its points to two fixed points is a constant. When the two fixed points coincide, a circle results.
- A curve of constant width is a figure whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines. The circle is the simplest example of this type of figure.
See also
- Affine sphere
- Annulus (mathematics)
- List of circle topics
- Loop
- Sphere
References
- ^ Chronology for 30000 BC to 500 BC
- ^ Squaring the circle
- ^ Measurement of a Circle by Archimedes
- ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007.
- ^ Harkness, James (1898). Introduction to the theory of analytic functions. London, New York: Macmillan and Co.. pp. 30. http://dlxs2.library.cornell.edu/cgi/t/text/text-idx?c=math;idno=01680002.
- ^ Ogilvy, C. Stanley, Excursions in Geometry, Dover, 1969, 14–17.
- ^ Altshiller-Court, Nathan, College Geometry, Dover, 2007 (orig. 1952).
Further reading
- Pedoe, Dan (1988). Geometry: a comprehensive course. Dover.
- "Circle" in The MacTutor History of Mathematics archive
External links
- Circle (PlanetMath.org website)
- Weisstein, Eric W., "Circle" from MathWorld.
- Interactive Java applets for the properties of and elementary constructions involving circles.
- Interactive Standard Form Equation of Circle Click and drag points to see standard form equation in action
- Munching on Circles at cut-the-knot
- MathAce's Circle article – has a good in-depth explanation of unit circles and transforming circular equations.
Categories:- Circles
- Elementary shapes
- Curves
- Conic sections
- Pi
-
Wikimedia Foundation. 2010.



















![|[A,B;C,P]| = 1.\](0/9e035e9d62f94ddf78be8760a6482aab.png)