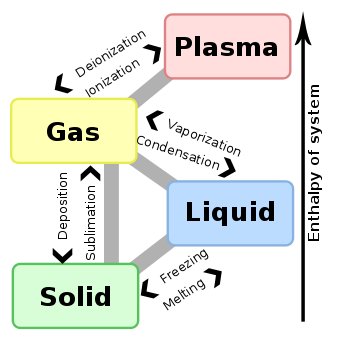
- Phase transition
-
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.
A phase of a thermodynamic system and the states of matter have uniform physical properties.
During a phase transition of a given medium certain properties of the medium change, often discontinuously, as a result of some external condition, such as temperature, pressure, and others. For example, a liquid may become gas upon heating to the boiling point, resulting in an abrupt change in volume. The measurement of the external conditions at which the transformation occurs is termed the phase transition point.
Phase transitions are common occurrences observed in nature and many engineering techniques exploit certain types of phase transition.
The term is most commonly used to describe transitions between solid, liquid and gaseous states of matter, in rare cases including plasma.
Contents
Types of phase transition
- The transitions between the solid, liquid, and gaseous phases of a single component, due to the effects
To From Solid Liquid Gas Plasma Solid Solid-solid transformation Melting/fusion Sublimation N/A Liquid Freezing N/A Boiling/evaporation N/A Gas Deposition Condensation N/A Ionization Plasma N/A N/A Recombination/deionization N/A -
- (see also vapor pressure and phase diagram)
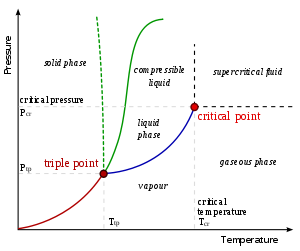 A typical phase diagram. The dotted line gives the anomalous behavior of water.
A typical phase diagram. The dotted line gives the anomalous behavior of water.
- A eutectic transformation, in which a two component single phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation.
- A peritectic transformation, in which a two component single phase solid is heated and transforms into a solid phase and a liquid phase.
- A spinodal decomposition, in which a single phase is cooled and separates into two different compositions of that same phase.
- Transition to a mesophase between solid and liquid, such as one of the "liquid crystal" phases.
- The transition between the ferromagnetic and paramagnetic phases of magnetic materials at the Curie point.
- The transition between differently ordered, commensurate or incommensurate, magnetic structures, such as in cerium antimonide.
- The martensitic transformation which occurs as one of the many phase transformations in carbon steel and stands as a model for displacive phase transformations.
- Changes in the crystallographic structure such as between ferrite and austenite of iron.
- Order-disorder transitions such as in alpha-titanium aluminides.
- The emergence of superconductivity in certain metals when cooled below a critical temperature.
- The transition between different molecular structures (polymorphs or allotropes), especially of solids, such as between an amorphous structure and a crystal structure or between two different crystal structures.
- Quantum condensation of bosonic fluids, such as Bose-Einstein condensation and the superfluid transition in liquid helium.
- The breaking of symmetries in the laws of physics during the early history of the universe as its temperature cooled.
Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are too small.
At the phase transition point (for instance, boiling point) the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.
It is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e. not theoretically stable, but quasistable. This occurs in superheating, supercooling and supersaturation.
Classifications
Ehrenfest classification
Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables. Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable.[1] The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the first derivative of the free energy with respect to chemical potential. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy.[1] These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.
Though useful, Ehrenfest's classification has been found to be an inaccurate method of classifying phase transitions, for it does not take into account the case where a derivative of free energy diverges (which is only possible in the thermodynamic limit). For instance, in the ferromagnetic transition, the heat capacity diverges to infinity.
Modern classifications
In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:
First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not. Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles).
Second-order phase transitions are also called continuous phase transitions. They are characterized by a divergent susceptibility, an infinite correlation length, and a power-law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconductor and the superfluid transition. Lev Landau gave a phenomenological theory of second order phase transitions.
Several transitions are known as the infinite-order phase transitions. They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions in two-dimensional electron gases belong to this class.
The liquid-glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. However, there is a longstanding debate whether there is an underlying second-order phase transition in the hypothetical limit of infinitely long relaxation times.
Characteristic properties
Critical points
In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).
Symmetry
Order parameters
The order parameter is normally a quantity which is 0 in one phase (usually above the critical point), and non-zero in the other. It characterises the onset of order at the phase transition. The order parameter susceptibility will usually diverge approaching the critical point. For a ferromagnetic system undergoing a phase transition, the order parameter is the net magnetization. For liquid/gas transitions, the order parameter is related to the density.
When symmetry is broken, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. Such variables are examples of order parameters. An order parameter is a measure of the degree of order in a system; the extreme values are 0 for total disorder and 1 for complete order.[2] For example, an order parameter can indicate the degree of order in a liquid crystal. However, note that order parameters can also be defined for non-symmetry-breaking transitions. Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.
There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect[disambiguation needed
 ] lines.
] lines.Relevance in cosmology
Symmetry-breaking phase transitions play an important role in cosmology. It has been speculated that, in the hot early universe, the vacuum (i.e. the various quantum fields that fill space) possessed a large number of symmetries. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis.)
Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[3] and David Layzer.[4] See also Relational order theories.
See also: Order-disorderCritical exponents and universality classes
Main article: critical exponentContinuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.
It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc. When T is near Tc, the heat capacity C typically has a power law behavior:
A similar behavior, but with the exponent ν instead of α, applies for the correlation length.
The exponent ν is positive. This is different with α. Its actual value depends on the type of phase transition we are considering.
For -1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003. At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample.[5] This experimental value of α agrees with theoretical predictions based on variational perturbation theory.[6]
For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the enthalpy stays finite). An example of such behavior is the 3-dimensional ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ +0.110.
Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.
Several other critical exponents - β, γ, δ, ν, and η - are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations such as β = γ / (δ − 1), ν = γ / (2 − η). It can be shown that there are only two independent exponents, e.g. ν and η.
It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid-gas critical point have been found to be independent of the chemical composition of the fluid. More amazingly, but understandable from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergency of the correlation length is the essential point.
Critical slowing down and other phenomena
There are also other critical phenoma; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.
Percolation Theory
Another phenomenon which shows phase transitions and critical exponents is percolation. The simplest example is perhaps percolation in a two dimensional square lattice. Sites are randomly occupied with probability p. For small values of p the occupied sites form only small clusters. At a certain threshold pc a giant cluster is formed and we have a second order phase transition.[7] The behavior of P∞ near pc is, P∞~(p-pc)β, where β is a critical exponent.
See also
- Allotropy
- Autocatalytic reactions and order creation
- Crystal growth
- Differential scanning calorimetry
- Diffusionless transformations
- Ehrenfest equations
- Jamming (physics)
- Kelvin probe force microscope
- Lambda transition universality class
- Landau theory of second order phase transitions
- Laser-heated pedestal growth
- List of states of matter
- Micro-Pulling-Down
- Percolation
- Phase separation
- Superfluid film
References
- ^ a b Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0198567707.
- ^ A. D. McNaught and A. Wilkinson, ed. "Compendium of Chemical Terminology (commonly called The Gold Book)". IUPAC. ISBN 0-86542-684-8. http://www.iupac.org/goldbook/O04323.pdf. Retrieved 2007-10-23.
- ^ Chaisson, “Cosmic Evolution”, Harvard, 2001
- ^ David Layzer, Cosmogenesis, The Development of Order in the Universe", Oxford Univ. Press, 1991
- ^ Arxiv.org
- ^ Prola.aps.org
- ^ Armin Bunde and Shlomo Havlin (1996). Fractals and Disordered Systems. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php.
Further reading
- Anderson, P.W., Basic Notions of Condensed Matter Physics, Perseus Publishing (1997).
- Goldenfeld, N., Lectures on Phase Transitions and the Renormalization Group, Perseus Publishing (1992).
- Krieger, Martin H., Constitutions of matter : mathematically modelling the most everyday of physical phenomena, University of Chicago Press, 1996. Contains a detailed pedagogical discussion of Onsager's solution of the 2-D Ising Model.
- Landau, L.D. and Lifshitz, E.M., Statistical Physics Part 1, vol. 5 of Course of Theoretical Physics, Pergamon, 3rd Ed. (1994).
- Kleinert, H., Critical Properties of φ4-Theories, World Scientific (Singapore, 2001); Paperback ISBN 981-02-4659-5 (readable online here).
- Kleinert, H. and Verena Schulte-Frohlinde, Gauge Fields in Condensed Matter, Vol. I, "Superfluid and Vortex lines; Disorder Fields, Phase Transitions,", pp. 1–742, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (readable online physik.fu-berlin.de)
- Mussardo G., "Statistical Field Theory. An Introduction to Exactly Solved Models of Statistical Physics", Oxford University Press, 2010.
- Schroeder, Manfred R., Fractals, chaos, power laws : minutes from an infinite paradise, New York: W.H. Freeman, 1991. Very well-written book in "semi-popular" style—not a textbook—aimed at an audience with some training in mathematics and the physical sciences. Explains what scaling in phase transitions is all about, among other things.
- Yeomans J. M., Statistical Mechanics of Phase Transitions, Oxford University Press, 1992.
- H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena (Oxford University Press, Oxford and New York 1971).
External links
- Interactive Phase Transitions on lattices with Java applets
- Theory of Reflexivity
States of matter Low energy High energy Other states Colloid · Glass · Liquid crystal · Magnetically ordered (Antiferromagnet, Ferrimagnet, Ferromagnet) · String-net liquid · SuperglassTransitions Boiling · Boiling point · Critical line · Critical point · Crystallization · Deposition · Evaporation · Flash evaporation · Freezing · Lambda point · Melting · Melting point · Regelation · Saturated fluid · Sublimation · Supercooling · Triple pointQuantities Enthalpy of fusion · Enthalpy of sublimation · Enthalpy of vaporization · Latent heat · Latent internal energy · Trouton's constant · Trouton's ratio · VolatilityConcepts Binodal · Compressed fluid · Cooling curve · Equation of state · Leidenfrost effect · Mpemba effect · Order and disorder (physics) · Spinodal · Superconductivity · Superheated vapor · Superheating · Thermo-dielectric effectCategories:- Fundamental physics concepts
- Phase changes
- Critical phenomena
Wikimedia Foundation. 2010.