- Uniform distribution (discrete)
-
discrete uniform Probability mass function
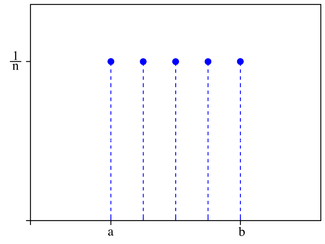
n = 5 where n = b − a + 1Cumulative distribution function
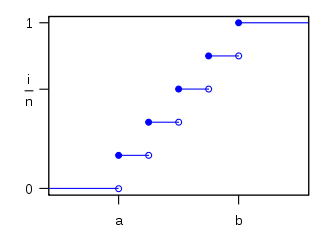
parameters: 


support: 
pmf: 
cdf: 
mean: 
median: 
mode: N/A variance: 
skewness: 
ex.kurtosis: 
entropy: 
mgf: 
cf: 
In probability theory and statistics, the discrete uniform distribution is a probability distribution whereby a finite number of equally spaced values are equally likely to be observed; every one of n values has equal probability 1/n. Another way of saying "discrete uniform distribution" would be "a known, finite number of equally spaced outcomes equally likely to happen."
If a random variable has any of n possible values
 that are equally spaced and equally probable, then it has a discrete uniform distribution. The probability of any outcome ki is 1 / n. A simple example of the discrete uniform distribution is throwing a fair die. The possible values of k are 1, 2, 3, 4, 5, 6; and each time the die is thrown, the probability of a given score is 1/6. If two dice are thrown and their values added, the uniform distribution no longer fits since the values from 2 to 12 do not have equal probabilities.
that are equally spaced and equally probable, then it has a discrete uniform distribution. The probability of any outcome ki is 1 / n. A simple example of the discrete uniform distribution is throwing a fair die. The possible values of k are 1, 2, 3, 4, 5, 6; and each time the die is thrown, the probability of a given score is 1/6. If two dice are thrown and their values added, the uniform distribution no longer fits since the values from 2 to 12 do not have equal probabilities.The cumulative distribution function (CDF) can be expressed in terms of a degenerate distribution as
where the Heaviside step function H(x − x0) is the CDF of the degenerate distribution centered at x0, using the convention that H(0) = 1.
Contents
Estimation of maximum
Main article: German tank problemThis example is described by saying that a sample of k observations is obtained from a uniform distribution on the integers
 , with the problem being to estimate the unknown maximum N. This problem is commonly known as the German tank problem, following the application of maximum estimation to estimates of German tank production during World War II.
, with the problem being to estimate the unknown maximum N. This problem is commonly known as the German tank problem, following the application of maximum estimation to estimates of German tank production during World War II.The UMVU estimator for the maximum is given by
where m is the sample maximum and k is the sample size, sampling without replacement.[1][2] This can be seen as a very simple case of maximum spacing estimation.
The formula may be understood intuitively as:
- "The sample maximum plus the average gap between observations in the sample",
the gap being added to compensate for the negative bias of the sample maximum as an estimator for the population maximum.[notes 1]
This has a variance of[1]
so a standard deviation of approximately N / k, the (population) average size of a gap between samples; compare
 above.
above.The sample maximum is the maximum likelihood estimator for the population maximum, but, as discussed above, it is biased.
If samples are not numbered but are recognizable or markable, one can instead estimate population size via the capture-recapture method.
Random permutation
Main article: Random permutationSee rencontres numbers for an account of the probability distribution of the number of fixed points of a uniformly distributed random permutation.
See also
- Delta distribution
- Uniform distribution (continuous)
Notes
- ^ The sample maximum is never more than the population maximum, but can be less, hence it is a biased estimator: it will tend to underestimate the population maximum.
References
- ^ a b Johnson, Roger (1994), "Estimating the Size of a Population", Teaching Statistics 16 (2 (Summer)): 50, doi:10.1111/j.1467-9639.1994.tb00688.x
- ^ Johnson, Roger (2006), "Estimating the Size of a Population", Getting the Best from Teaching Statistics, http://www.rsscse.org.uk/ts/gtb/johnson.pdf
Some common univariate probability distributions Continuous Discrete - Bernoulli
- binomial
- discrete uniform
- geometric
- hypergeometric
- negative binomial
- Poisson
Categories:- Discrete distributions
Wikimedia Foundation. 2010.



