- Differential geometry of surfaces
-
 Carl Friedrich Gauss in 1828
Carl Friedrich Gauss in 1828
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss (1825-1827), who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
Surfaces naturally arise as graphs of functions of a pair of variables, and sometimes appear in parametric form or as loci associated to space curves. An important role in their study has been played by Lie groups (in the spirit of the Erlangen program), namely the symmetry groups of the Euclidean plane, the sphere and the hyperbolic plane. These Lie groups can be used to describe surfaces of constant Gaussian curvature; they also provide an essential ingredient in the modern approach to intrinsic differential geometry through connections. On the other hand extrinsic properties relying on an embedding of a surface in Euclidean space have also been extensively studied. This is well illustrated by the non-linear Euler-Lagrange equations in the calculus of variations: although Euler developed the one variable equations to understand geodesics, defined independently of an embedding, one of Lagrange's main applications of the two variable equations was to minimal surfaces, a concept that can only be defined in terms of an embedding.
Overview
See also: SurfacesPolyhedra in the Euclidean space, such as the boundary of a cube, are among the first surfaces encountered in geometry. It is also possible to define smooth surfaces, in which each point has a neighborhood diffeomorphic to some open set in E2, the Euclidean plane. This elaboration allows calculus to be applied to surfaces to prove many results.
Two smooth surfaces are diffeomorphic if and only if they are homeomorphic. (The analogous result does not hold for higher-dimensional manifolds.) It follows that closed surfaces are classified up to diffeomorphism by their Euler characteristic and orientability.
Smooth surfaces equipped with Riemannian metrics are of foundational importance in differential geometry. A Riemannian metric endows a surface with notions of geodesic, distance, angle, and area. An important class of such surfaces are the developable surfaces: surfaces that can be flattened to a plane An without stretching; examples include the cylinder and the cone.
In addition, there are properties of surfaces which depend on an embedding of the surface into Euclidean space. These surfaces are the subject of extrinsic geometry. They include
- Minimal surfaces are surfaces that minimize the surface area for given boundary conditions; examples include soap films stretched across a wire frame, catenoids and helicoids.
- Ruled surfaces are surfaces that have at least one straight line running through every point; examples include the cylinder and the hyperboloid of one sheet.
Any n-dimensional complex manifold is, at the same time, a real (2n)-dimensional real manifold. Thus any complex one-manifold (also called a Riemann surface) is a smooth oriented surface with an associated complex structure[disambiguation needed
 ]. Every closed surface admits complex structures. Any complex algebraic curve or real algebraic surface is also a smooth surface, possibly with singularities.
]. Every closed surface admits complex structures. Any complex algebraic curve or real algebraic surface is also a smooth surface, possibly with singularities.Complex structures on a closed oriented surface correspond to conformal equivalence classes of Riemannian metrics on the surface. One version of the uniformization theorem (due to Poincaré) states that any Riemannian metric on an oriented, closed surface is conformally equivalent to an essentially unique metric of constant curvature. This provides a starting point for one of the approaches to Teichmüller theory, which provides a finer classification of Riemann surfaces than the topological one by Euler characteristic alone.
The uniformization theorem states that every smooth Riemannian surface S is conformally equivalent to a surface having constant curvature, and the constant may be taken to be 1, 0, or -1. A surface of constant curvature 1 is locally isometric to the sphere, which means that every point on the surface has an open neighborhood that is isometric to an open set on the unit sphere in E3 with its intrinsic Riemannian metric. Likewise, a surface of constant curvature 0 is locally isometric to the Euclidean plane, and a surface of constant curvature -1 is locally isometric to the hyperbolic plane.
Constant curvature surfaces are the two-dimensional realization of what are known as space forms. These are often studied from the point of view of Felix Klein's Erlangen programme, by means of smooth transformation groups. Any connected surface with a three-dimensional group of isometries is a surface of constant curvature.
A complex surface is a complex two-manifold and thus a real four-manifold; it is not a surface in the sense of this article. Neither are algebraic curves or surfaces defined over fields other than the complex numbers.
History of surfaces
Isolated properties of surfaces of revolution were known already to Archimedes. The development of calculus in the seventeenth century provided a more systematic way of proving them. Curvature of general surfaces was first studied by Euler. In 1760[1] he proved a formula for the curvature of a plane section of a surface and in 1771[2] he considered surfaces represented in a parametric form. Monge laid down the foundations of their theory in his classical memoir L'application de l'analyse à la géometrie which appeared in 1795. The defining contribution to the theory of surfaces was made by Gauss in two remarkable papers written in 1825 and 1827.[3] This marked a new departure from tradition because for the first time Gauss considered the intrinsic geometry of a surface, the properties which are determined only by the geodesic distances between points on the surface independently of the particular way in which the surface is located in the ambient Euclidean space. The crowning result, the Theorema Egregium of Gauss, established that the Gaussian curvature is an intrinsic invariant, i.e. invariant under local isometries. This point of view was extended to higher-dimensional spaces by Riemann and led to what is known today as Riemannian geometry. The nineteenth century was the golden age for the theory of surfaces, from both the topological and the differential-geometric point of view, with most leading geometers devoting themselves to their study.[citation needed] Darboux collected many results in his four-volume treatise Théorie des surfaces (1887–1896).
The presentation below largely follows Gauss, but with important later contributions from other geometers. For a time Gauss was Cartographer to George III of Great Britain and Hannover; this royal patronage could explain why these papers contain practical calculations of the curvature of the earth based purely on measurements on the surface of the planet.
Curvature of surfaces in E3
See also: Gaussian curvature and Mean curvatureInformally Gauss defined the curvature of a surface in terms of the curvatures of certain plane curves connected with the surface. He later found a series of equivalent definitions. One of the first was in terms of the area-expanding properties of the Gauss map, a map from the surface to a 2-dimensional sphere. However, before obtaining a more intrinsic definition in terms of the area and angles of small triangles, Gauss needed to make an in-depth investigation of the properties of geodesics on the surface, i.e. paths of shortest length between two fixed points on the surface[4] (see below).
The Gaussian curvature at a point on an embedded smooth surface given locally by the equation
- z = F(x,y)
in E3, is defined to be the product of the principal curvatures at the point;[5] the mean curvature is defined to be their sum. The principal curvatures are the maximum and minimum curvatures of the plane curves obtained by intersecting the surface with planes normal to the tangent plane at the point. If the point is (0, 0, 0) with tangent plane z = 0, then, after a rotation about the z-axis setting the coefficient on xy to zero, F will have the Taylor series expansion
The principal curvatures are k1 and k2 in this case, the Gaussian curvature is given by
and the mean curvature by
-
Km = k1 + k2.
Since K and Km are invariant under isometries of E3, in general
-
K = (RT − S2)/(1 + P2 + Q2)2
and
-
Km =(ET + GR – 2FS)/(1 + P2 + Q2)2
where the derivatives at the point are given by P = Fx, Q = Fy, R = Fx x, S = Fx y, and T = Fy y.[6]
For every oriented embedded surface the Gauss map is the map into the unit sphere sending each point to the (outward pointing) unit normal vector to the oriented tangent plane at the point. In coordinates the map sends (x,y,z) to
- N(x, y, z) = (P2 + Q2 + 1)−1/2·(P, Q, −1).
Direct computation shows that[7]
- the Gaussian curvature is the Jacobian of the Gauss map.
Examples
Surfaces of revolution
Main article: Surface of revolutionA surface of revolution can be obtained by rotating a curve in the xz plane about the z-axis, assuming the curve does not intersect the z-axis. Suppose that the curve is given by
with t lies in (a, b), and is parametrized by arclength, so that
Then the surface of revolution is the point set
The Gaussian curvature and mean curvature are given by[8]
 A quadric ellipsoid
A quadric ellipsoid
Geodesics on a surface of revolution are governed by Clairaut's relation.
Quadric surfaces
Main article: Quadric surfaceConsider the quadric surface defined by[9]
This surface admits a parametrization
The Gaussian curvature and mean curvature are given by
 A single-sheeted quadric hyperboloid which is a ruled surface in two different ways.
A single-sheeted quadric hyperboloid which is a ruled surface in two different ways.
Ruled surfaces
Main article: Ruled surfaceA ruled surface is one which can be generated by the motion of a straight line in E3.[10] Choosing a directrix on the surface, i.e. a smooth unit speed curve c(t) orthogonal to the straight lines, and then choosing u(t) to be unit vectors along the curve in the direction of the lines, the velocity vector v=ct and u satisfy
The surface consists of points
as s and t vary.
Then, if
the Gaussian and mean curvature are given by
The Gaussian curvature of the ruled surface vanishes if and only if ut and v are proportional,[11] This condition is equivalent to the surface being the envelope of the planes along the curve containing the tangent vector v and the orthogonal vector u, i.e. to the surface being developable along the curve.[12] More generally a surface in E3 has vanishing Gaussian curvature near a point if and only if it is developable near that point.[6] (An equivalent condition is given below in terms of the metric.)
Minimal surfaces
Main article: Minimal surfaceIn 1760 Lagrange extended Euler's results on the calculus of variations involving integrals in one variable to two variables.[13] He had in mind the following problem:
Given a closed curve in E3, find a surface having the curve as boundary with minimal area.
Such a surface is called a minimal surface. In 1776 Jean Baptiste Meusnier showed that the differential equation derived by Lagrange was equivalent to the vanishing of the mean curvature of the surface:
A surface is minimal if and only if its mean curvature vanishes.
Minimal surfaces have a simple interpretation in real life: they are the shape a soap film will assume if a wire frame shaped like the curve is dipped into a soap solution and then carefully lifted out. The question as to whether a minimal surface with given boundary exists is called Plateau's problem after the Belgian physicist Joseph Plateau who carried out experiments on soap films in the mid-nineteenth century. In 1930 Jesse Douglas and Tibor Radó gave an affirmative answer to Plateau's problem (Douglas was awarded one of the first Fields medals for this work in 1936).[14]
Many explicit examples of minimal surface are known explicitly, such as the catenoid, the helicoid, the Scherk surface and the Enneper surface. There has been extensive research in this area, summarised in Osserman (2002). In particular a result of Osserman shows that if a minimal surface is non-planar, then its image under the Gauss map is dense in S2.
Surfaces of constant Gaussian curvature
If a surface has constant Gaussian curvature, it is called a surface of constant curvature.[15]
- The unit sphere in E3 has constant Gaussian curvature +1.
- The Euclidean plane and the cylinder both have constant Gaussian curvature 0.
- The surfaces of revolution with φtt = φ have constant Gaussian curvature –1. Particular cases are obtained by taking φ(t) = C cosh t, C sinh t and C et.[16] The latter case is the classical pseudosphere generated by rotating a tractrix around a central axis. In 1868 Beltrami showed that the geometry of the pseudosphere was directly related to that of the hyperbolic plane, discovered independently by Lobachevsky (1830) and Bolyai (1832) . Already in 1840, F. Minding, a student of Gauss, had obtained trigonometric formulas for the pseudosphere identical to those for the hyperbolic plane.[17] This surface of constant curvature is now better understood in terms of the Poincaré metric on the upper half plane or the unit disc, and has been described by other models such as the Klein model or the hyperboloid model, obtained by considering the two-sheeted hyperboloid q(x, y, z) = −1 in three-dimensional Minkowski space, where q(x, y, z) = x2 + y2 – z2.[18]
Each of these surfaces of constant curvature has a transitive Lie group of symmetries. This group theoretic fact has far-reaching consequences, all the more remarkable because of the central role these special surfaces play in the geometry of surfaces, due to Poincaré's uniformization theorem (see below).
Other examples of surfaces with Gaussian curvature 0 include cones, tangent developables, and more generally any developable surface.
Local metric structure
Main article: Riemannian manifoldFor any surface embedded in Euclidean space of dimension 3 or higher, it is possible to measure the length of a curve on the surface, the angle between two curves and the area of a region on the surface. This structure is encoded infinitesimally in a Riemannian metric on the surface through line elements and area elements. Classically in the nineteenth and early twentieth centuries only surfaces embedded in R3 were considered and the metric was given as a 2 x 2 positive definite matrix varying smoothly from point to point in a local parametrization of the surface. The idea of local parametrization and change of coordinate was later formalized through the current abstract notion of a manifold, a topological space where the smooth structure is given by local charts on the manifold, exactly as the planet Earth is mapped by atlases today. Changes of coordinates between different charts of the same region are required to be smooth. Just as contour lines on real-life maps encode changes in elevation, taking into account local distortions of the Earth's surface to calculate true distances, so the Riemannian metric describes distances and areas "in the small" in each local chart. In each local chart a Riemannian metric is given by smoothly assigning a 2 x 2 positive definite matrix to each point; when a different chart is taken, the matrix is transformed according to the Jacobian matrix of the coordinate change. The manifold then has the structure of a 2-dimensional Riemannian manifold.
Line and area elements
Taking a local chart, for example by projecting onto the x-y plane (z = 0), the line element ds and the area element dA can be written in terms of local coordinates as
- ds2 = E dx2 + 2F dx dy + G dy2
and
- dA = (EG − F2)1/2 dx dy.
The expression E dx2 + 2F dx dy + G dy2 is called the first fundamental form.[6]
The matrix
is required to be positive-definite and to depend smoothly on x and y.
In a similar way line and area elements can be associated to any abstract Riemannian 2-manifold in a local chart.
Second fundamental form
Main article: Second fundamental formThe extrinsic geometry of surfaces studies the properties of surfaces embedded into a Euclidean space, typically E3. In intrinsic geometry, two surfaces are "the same" if it is possible to unfold one surface onto the other without stretching it, i.e. a map of one surface onto the other preserving distance. Thus a cylinder is locally "the same" as the plane. In extrinsic geometry, two surfaces are "the same" if they are congruent in the ambient Euclidean space, i.e. there is an isometry of E3 carrying one surface onto the other. With this more rigid definition of similitude, the cylinder and the plane are obviously no longer the same.
Although the primary invariant in the study of the intrinsic geometry of surfaces is the metric (the first fundamental form) and the Gaussian curvature, certain properties of surfaces also depend on an embedding into E3 (or a higher dimensional Euclidean space). The most important example is the second fundamental form, defined classically as follows.[19]
Take a point (x, y) on the surface in a local chart. The square of the Euclidean distance from a nearby point (x + dx, y + dy) to the tangent plane at (x, y), i.e. the square of the length of the perpendicular dropped from the nearby point to the tangent plane, has the form
- e dx2 + 2f dx dy + g dy2
plus third and higher order corrections. The above expression, a symmetric bilinear form at each point, is the second fundamental form. It is described by a 2 × 2 symmetric matrix
which depends smoothly on x and y. The Gaussian curvature can be calculated as the ratio of the determinants of the second and first fundamental forms:
Remarkably Gauss proved that it is an intrinsic invariant (see his Theorema Egregium below).
One of the other extrinisic numerical invariants of a surface is the mean curvature Km, defined as the sum of the principal curvatures. It is given by the formula[6]
The coefficients of the first and second fundamental forms satisfy certain compatibility conditions known as the Gauss-Codazzi equations; they involve the Christoffel symbols
 associated with the first fundamental form:[20]
associated with the first fundamental form:[20]These equations can also be succinctly expressed and derived in the language of connection forms due to Élie Cartan.[21] Pierre Bonnet proved that two quadratic forms satisfying the Gauss-Codazzi equations always uniquely determine an embedded surface locally.[22] For this reason the Gauss-Codazzi equations are often called the fundamental equations for embedded surfaces, precisely identifying where the intrinsic and extrinsic curvatures come from. They admit generalizations to surfaces embedded in more general Riemannian manifolds.
Shape operator
The differential df of the Gauss map f can be used to define a type of extrinsic curvature, known as the shape operator[23] or Weingarten map. This operator first appeared implicitly in the work of Wilhelm Blaschke and later explicitly in a treatise by Burali-Forti and Burgati.[24] Since at each point x of the surface, the tangent space is an inner product space, the shape operator Sx can be defined as a linear operator on this space by the formula
- (Sxv,w) = (df(v),w)
for tangent vectors v, w (the inner product makes sense because df(v) and w both lie in E3).[25] The right hand side is symmetric in v and w, so the shape operator is self-adjoint on the tangent space. The eigenvalues of Sx are just the principal curvatures k1 and k2 at x. In particular the determinant of the shape operator at a point is the Gaussian curvature, but it also contains other information, since the mean curvature is half the trace of the shape operator. The mean curvature is an extrinsic invariant. In intrinsic geometry, a cylinder is developable, meaning that every piece of it is intrinsically indistinguishable from a piece of a plane since its Gauss curvature vanishes identically. Its mean curvature is not zero, though; hence extrinsically it is different from a plane.
In general, the eigenvectors and eigenvalues of the shape operator at each point determine the directions in which the surface bends at each point. The eigenvalues correspond to the principal curvatures of the surface and the eigenvectors are the corresponding principal directions. The principal directions specify the directions that a curve embedded in the surface must travel to have maximum and minimum curvature, these being given by the principal curvatures.
The shape operator is given in terms of the components of the first and second fundamental forms by the Weingarten equations:[26]
Geodesic curves on a surface
Curves on a surface which minimize length between the endpoints are called geodesics; they are the shape that an elastic band stretched between the two points would take. Mathematically they are described using partial differential equations from the calculus of variations. The differential geometry of surfaces revolves around the study of geodesics. It is still an open question whether every Riemannian metric on a 2-dimensional local chart arises from an embedding in 3-dimensional Euclidean space: the theory of geodesics has been used to show this is true in the important case when the components of the metric are analytic.
Geodesics
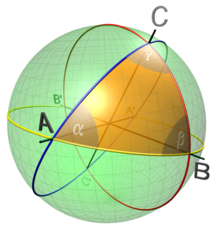
 A geodesic triangle on the sphere. The geodesics are great circle arcs.
A geodesic triangle on the sphere. The geodesics are great circle arcs.
Given a piecewise smooth path c(t) = (x(t), y(t)) in the chart for t in [a, b], its length is defined by
and energy by
The length is independent of the parametrisation of a path. By the Euler-Lagrange equations, if c(t) is a path minimising length, parametrised by arclength, it must satisfy the Euler equations
 + Γ¹11
+ Γ¹11 ² + 2Γ¹12
² + 2Γ¹12  + Γ¹22
+ Γ¹22  ² =0 and
² =0 and  + Γ²11
+ Γ²11 ² + 2Γ²12
² + 2Γ²12  + Γ²22
+ Γ²22  ² =0
² =0
where the Christoffel symbols Γkij are given by
- Γkij =
 g km (
g km ( j gim +
j gim + i gjm –
i gjm –  m gij)
m gij)
where g11 = E, g12=F, g22 =G and (gij) is the inverse matrix to (gij). A path satisfying the Euler equations is called a geodesic. By the Cauchy-Schwarz inequality a path minimising energy is just a geodesic parametrised by arc length; and, for any geodesic, the parameter t is proportional to arclength.[27]
Geodesic curvature
See also: Geodesic curvature and Darboux frameThe geodesic curvature kg at a point of a curve c(t), parametrised by arc length, on an oriented surface is defined to be[28]
where n(t) is the "principal" unit normal to the curve in the surface, constructed by rotating the unit tangent vector
 through an angle of + 90°.
through an angle of + 90°.- The geodesic curvature at a point is an intrinsic invariant depending only on the metric near the point.
- A unit speed curve on a surface is a geodesic if and only if its geodesic curvature vanishes at all points on the curve.
- A unit speed curve c(t) in an embedded surface is a geodesic if and only if its acceleration vector
 is normal to the surface.
is normal to the surface.
The geodesic curvature measures in a precise way how far a curve on the surface is from being a geodesic.
Isometric embedding problem
A result of Jacobowitz (1972) and Poznjak (1973) shows that every metric structure on a surface arises from a local embedding in E4. Apart from some special cases, whether this is possible in E3 remains an open question, the so-called "Weyl problem".[29] In 1926 Maurice Janet proved that it is always possible locally if E, F and G are analytic; soon afterwards Élie Cartan generalised this to local embeddings of Riemannian n-manifolds in Em where m = ½(n² +n). To prove Janet's theorem near (0,0), the Cauchy-Kowalevski theorem is used twice to produce analytic geodesics orthogonal to the y-axis and then the x-axis to make an analytic change of coordinate so that E=1 and F=0. An isometric embedding u must satisfy
- ux • ux =1, ux • uy = 0, uy • uy = G.
Differentiating gives the three additional equations
- uxx • uy = 0, uxx • ux = 0, uxx • uyy = uxy • ux y - ½ Gxx
with u(0,y) and ux(0,y) prescribed. These equations can be solved near (0,0) using the Cauchy-Kowalevski theorem and yield a solution of the original embedding equations.
Orthogonal coordinates
When F=0 in the metric, lines parallel to the x- and y-axes are orthogonal and provide orthogonal coordinates. If H=(EG)½, then the Gaussian curvature is given by[30]
If in addition E=1, so that H=G½, then the angle φ at the intersection between geodesic (x(t),y(t)) and the line y = constant is given by the equation
The derivative of φ is given by a classical derivative formula of Gauss:[31]
Geodesic polar coordinates
Once a metric is given on a surface and a base point is fixed, there is a unique geodesic connecting the base point to each sufficiently nearby point. The direction of the geodesic at the base point and the distance uniquely determine the other endpoint. These two bits of data, a direction and a magnitude, thus determine a tangent vector at the base point. The map from tangent vectors to endpoints smoothly sweeps out a neighbourhood of the base point and defines what is called the "exponential map", defining a local coordinate chart at that base point. The neighbourhood swept out has similar properties to balls in Euclidean space, namely any two points in it are joined by a unique geodesic. This property is called "geodesic convexity" and the coordinates are called "normal coordinates". The explicit calculation of normal coordinates can be accomplished by considering the differential equation satisfied by geodesics. The convexity properties are consequences of Gauss's lemma and its generalisations. Roughly speaking this lemma states that geodesics starting at the base point must cut the spheres of fixed radius centred on the base point at right angles. Geodesic polar coordinates are obtained by combining the exponential map with polar coordinates on tangent vectors at the base point. The Gaussian curvature of the surface is then given by the second order deviation of the metric at the point from the Euclidean metric. In particular the Gaussian curvature is an invariant of the metric, Gauss's celebrated Theorema Egregium. A convenient way to understand the curvature comes from an ordinary differential equation, first considered by Gauss and later generalized by Jacobi, arising from the change of normal coordinates about two different points. The Gauss–Jacobi equation provides another way of computing the Gaussian curvature. Geometrically it explains what happens to geodesics from a fixed base point as the endpoint varies along a small curve segment through data recorded in the Jacobi field, a vector field along the geodesic.[32] One and a quarter centuries after Gauss and Jacobi, Marston Morse gave a more conceptual interpretation of the Jacobi field in terms of second derivatives of the energy function on the infinite-dimensional Hilbert manifold of paths.[33]
Exponential map
Main article: Normal coordinatesThe theory of ordinary differential equations shows that if f(t, v) is smooth then the differential equation dv/dt = f(t,v) with initial condition v(0) = v0 has a unique solution for |t| sufficiently small and the solution depends smoothly on t and v0. This implies that for sufficiently small tangent vectors v at a given point p = (x0,y0), there is a geodesic cv(t) defined on (−2,2) with cv(0) = (x0,y0) and
 v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by
v(0) = v. Moreover if |s| ≤ 1, then csv = cv(st). The exponential map is defined by- expp(v) = cv (1)
and gives a diffeomorphism between a disc ||v|| < δ and a neighbourhood of p; more generally the map sending (p,v) to expp(v) gives a local diffeomorphism onto a neighbourhood of (p,p). The exponential map gives geodesic normal coordinates near p.[34]
Computation of normal coordinates
There is a standard technique (see for example Berger (2004)) for computing the change of variables to normal coordinates u, v at a point as a formal Taylor series expansion. If the coordinates x, y at (0,0) are locally orthogonal, write
- x(u,v) = α u + L(u,v) + λ(u,v) + ···
- y(u,v) = β v + M(u,v) + μ(u,v) + ···
where L, M are quadratic and λ, μ cubic homogeneous polynomials in u and v. If u and v are fixed, x(t) = x(tu,tv) and y(t) = y(tu, tv) can be considered as formal power series solutions of the Euler equations: this uniquely determines α, β, L, M, λ and μ.
Gauss's lemma
Main article: Gauss's lemma (Riemannian geometry)In these coordinates the matrix g(x) satisfies g(0) = I and the lines t ↦ tv are geodesics through 0. Euler's equations imply the matrix equation
- g(v)v = v,
a key result, usually called the Gauss lemma. Geometrically it states that
-
the geodesics through 0 cut the circles centred at 0 orthogonally.
Taking polar coordinates (r,θ), it follows that the metric has the form
- ds2 = dr2 + G(r,θ) dθ2.
In geodesic coordinates, it is easy to check that the geodesics through zero minimize length. The topology on the Riemannian manifold is then given by a distance function d(p,q), namely the infimum of the lengths of piecewise smooth paths between p and q. This distance is realised locally by geodesics, so that in normal coordinates d(0,v) = ||v||. If the radius δ is taken small enough, a slight sharpening of the Gauss lemma shows that the image U of the disc ||v|| < δ under the exponential map is geodesically convex, i.e. any two points in U are joined by a unique geodesic lying entirely inside U.[5]
Theorema Egregium
Main article: Theorema EgregiumTaking x and y coordinates of a surface in E3 corresponding to F(x,y) = k1 x2 + k2 y2 + ···, the power series expansion of the metric is given in normal coordinates (u, v) as
- ds2 = du2 + dv2 + K(u dv – v du)2 + ···
This extraordinary result — Gauss' Theorema Egregium — shows that the Gaussian curvature of a surface can be computed solely in terms of the metric and is thus an intrinsic invariant of the surface, independent of any embedding in E³ and unchanged under coordinate transformations. In particular isometries of surfaces preserve Gaussian curvature.[5]
Gauss–Jacobi equation
Main article: Jacobi fieldTaking a coordinate change from normal coordinates at p to normal coordinates at a nearby point q, yields the Sturm–Liouville equation satisfied by H(r,θ) = G(r,θ)½, discovered by Gauss and later generalised by Jacobi,
-
Hrr = – K H
The Jacobian of this coordinate change at q is equal to Hr. This gives another way of establishing the intrinsic nature of Gaussian curvature. Because H(r,θ) can be interpreted as the length of the line element in the θ direction, the Gauss–Jacobi equation shows that the Gaussian curvature measures the spreading of geodesics on a geometric surface as they move away from a point.[35]
Laplace–Beltrami operator
On a surface with local metric
and Laplace–Beltrami operator
where H2 = EG – F 2, the Gaussian curvature at a point is given by the formula[36]
where r is the denotes the geodesic distance from the point.
Since Δ is manifestly an intrinsic invariant, this gives yet another proof that the Gaussian curvature is an intrinsic invariant.
In isothermal coordinates, first considered by Gauss, the metric is required to be of the special form
In this case the Laplace–Beltrami operator is given by
and φ satisfies Liouville's equation[37]
Isothermal coordinates are known to exist in a neighbourhood of any point on the surface, although all proofs to date rely on non-trivial results on partial differential equations.[38] There is an elementary proof for minimal surfaces.[39]
Gauss–Bonnet theorem
 A triangulation of the torus
A triangulation of the torus
On a sphere or a hyperboloid, the area of a geodesic triangle, i.e. a triangle all the sides of which are geodesics, is proportional to the difference of the sum of the interior angles and π. The constant of proportionality is just the Gaussian curvature, a constant for these surfaces. For the torus, the difference is zero, reflecting the fact that its Gaussian curvature is zero. These are standard results in spherical, hyperbolic and high school trigonometry (see below). Gauss generalised these results to an arbitrary surface by showing that the integral of the Gaussian curvature over the interior of a geodesic triangle is also equal to this angle difference or excess. His formula showed that the Gaussian curvature could be calculated near a point as the limit of area over angle excess for geodesic triangles shrinking to the point. Since any closed surface can be decomposed up into geodesic triangles, the formula could also be used to compute the integral of the curvature over the whole surface. As a special case of what is now called the Gauss-Bonnet theorem, Gauss proved that this integral was remarkably always 2π times an integer, a topological invariant of the surface called the Euler characteristic. This invariant is easy to compute combinatorially in terms of the number of vertices, edges, and faces of the triangles in the decomposition, also called a triangulation. This interaction between analysis and topology was the forerunner of many later results in geometry, culminating in the Atiyah-Singer index theorem. In particular properties of the curvature impose restrictions on the topology of the surface.
Geodesic triangles
Gauss proved that, if Δ is a geodesic triangle on a surface with angles α, β and γ at vertices A, B and C, then
-
 Δ K dA = α + β + γ − π.
Δ K dA = α + β + γ − π.
In fact taking geodesic polar coordinates with origin A and AB, AC the radii at polar angles 0 and α
 Δ K dA =
Δ K dA = Δ KH dr dθ = –
Δ KH dr dθ = –  Hrr dr dθ =
Hrr dr dθ =  1 − Hr(rθ,θ) dθ =
1 − Hr(rθ,θ) dθ =  dθ +
dθ +  dφ = α + β + γ − π,
dφ = α + β + γ − π,
where the second equality follows from the Gauss–Jacobi equation and the fourth from Gauss' derivative formula in the orthogonal coordinates (r,θ).
Gauss' formula shows that the curvature at a point can be calculated as the limit of angle excess α + β + γ − π over area for successively smaller geodesic triangles near the point. Qualitatively a surface is positively or negatively curved according to the sign of the angle excess for arbitrarily small geodesic triangles.[6]
Gauss-Bonnet theorem
 The Euler characteristic of a sphere, triangulated like an icosahedron, is V - E + F = 12 - 30 + 20 =2.
The Euler characteristic of a sphere, triangulated like an icosahedron, is V - E + F = 12 - 30 + 20 =2. Main article: Gauss-Bonnet theorem
Main article: Gauss-Bonnet theoremSince every compact oriented 2-manifold M can be triangulated by small geodesic triangles, it follows that
-
 M K dA = 2π·χ(M)
M K dA = 2π·χ(M)
where χ(M) denotes the Euler characteristic of the surface.
In fact if there are F faces, E edges and V vertices, then 3F = 2E and the left hand side equals 2π·V – π·F = 2π·(V – E + F) = 2π·χ(M).
This is the celebrated Gauss-Bonnet theorem: it shows that the integral of the Gaussian curvature is a topological invariant of the manifold, namely the Euler characteristic. This theorem can be interpreted in many ways; perhaps one of the most far-reaching has been as the index theorem for an elliptic differential operator on M, one of the simplest cases of the Atiyah-Singer index theorem. Another related result, which can be proved using the Gauss-Bonnet theorem, is the Poincaré-Hopf index theorem for vector fields on M which vanish at only a finite number of points: the sum of the indices at these points equals the Euler characteristic. (On a small circle round each isolated zero, the vector field defines a map into the unit circle; the index is just the winding number of this map.)[6]
Curvature and embeddings
If the Gaussian curvature of a surface M is everywhere positive, then the Euler characteristic is positive so M is homeomorphic (and therefore diffeomorphic) to S2. If in addition the surface is isometrically embedded in E3, the Gauss map provides an explicit diffeomorphism. As Hadamard observed, in this case the surface is convex; this criterion for convexity can be viewed as a 2-dimensional generalisation of the well-known second derivative criterion for convexity of plane curves. Hilbert proved that every isometrically embedded closed surface must have a point of positive curvature. Thus a closed Riemannian 2-manifold of non-positive curvature can never be embedded isometrically in E3; however, as Adriano Garsia showed using the Beltrami equation for quasiconformal mappings, this is always possible for some conformally equivalent metric.[40]
Surfaces of constant curvature
The simply connected surfaces of constant curvature 0, +1 and –1 are the Euclidean plane, the unit sphere in E3, and the hyperbolic plane. Each of these has a transitive three-dimensional Lie group of orientation preserving isometries G, which can be used to study their geometry. Each of the two non-compact surfaces can be identified with the quotient G / K where K is a maximal compact subgroup of G. Here K is isomorphic to SO(2). Any other closed Riemannian 2-manifold M of constant Gaussian curvature, after scaling the metric by a constant factor if necessary, will have one of these three surfaces as its universal covering space. In the orientable case, the fundamental group Γ of M can be identified with a torsion-free uniform subgroup of G and M can then be identified with the double coset space Γ \ G / K. In the case of the sphere and the Euclidean plane, the only possible examples are the sphere itself and tori obtained as quotients of R2 by discrete rank 2 subgroups. For closed surfaces of genus
 , the moduli space of Riemann surfaces obtained as Γ varies over all such subgroups, has real dimension 6g - 6 .[41] By Poincaré's uniformization theorem, any orientable closed 2-manifold is conformally equivalent to a surface of constant curvature 0, +1 or –1. In other words, by multiplying the metric by a positive scaling factor, the Gaussian curvature can be made to take exactly one of these values (the sign of the Euler characteristic of M).[42]
, the moduli space of Riemann surfaces obtained as Γ varies over all such subgroups, has real dimension 6g - 6 .[41] By Poincaré's uniformization theorem, any orientable closed 2-manifold is conformally equivalent to a surface of constant curvature 0, +1 or –1. In other words, by multiplying the metric by a positive scaling factor, the Gaussian curvature can be made to take exactly one of these values (the sign of the Euler characteristic of M).[42]Euclidean geometry
In the case of the Euclidean plane, the symmetry group is the Euclidean motion group, the semidirect product of the two dimensional group of translations by the group of rotations.[43] Geodesics are straight lines and the geometry is encoded in the elementary formulas of trigonometry, such as the cosine rule for a triangle with sides a, b, c and angles α, β, γ:
Flat tori can be obtained by taking the quotient of R2 by a lattice, i.e. a free Abelian subgroup of rank 2. These closed surfaces have no isometric embeddings in E3. They do nevertheless admit isometric embeddings in E4; in the easiest case this follows from the fact that the torus is a product of two circles and each circle can be isometrically embedded in E2.[44]
Spherical geometry
See also: spherical trigonometry and spherical triangleThe isometry group of the unit sphere S2 in E3 is the orthogonal group O(3), with the rotation group SO(3) as the subgroup of isometries preserving orientation. It is the direct product of SO(3) with the antipodal map, sending x to –x.[45] The group SO(3) acts transitively on S2. The stabilizer subgroup of the unit vector (0,0,1) can be identified with SO(2), so that S2 = SO(3)/SO(2).
The geodesics between two points on the sphere are the great circle arcs with these given endpoints. If the points are not antipodal, there is a unique shortest geodesic between the points. The geodesics can also be described group theoretically: each geodesic through the North pole (0,0,1) is the orbit of the subgroup of rotations about an axis through antipodal points on the equator.
A spherical triangle is a geodesic triangle on the sphere. It is defined by points A, B, C on the sphere with sides BC, CA, AB formed from great circle arcs of length less than π. If the lengths of the sides are a, b, c and the angles between the sides α, β, γ, then the spherical cosine law states that
The area of the triangle is given by
- Area = α + β + γ - π.
Using stereographic projection from the North pole, the sphere can be identified with the extended complex plane C
 {∞}. The explicit map is given by
{∞}. The explicit map is given byUnder this correspondence every rotation of S2 corresponds to a Möbius transformation in SU(2), unique up to sign.[46] With respect to the coordinates (u, v) in the complex plane, the spherical metric becomes[47]
The unit sphere is the unique closed orientable surface with constant curvature +1. The quotient SO(3)/O(2) can be identified with the real projective plane. It is non-orientable and can be described as the quotient of S2 by the antipodal map (multiplication by –1). The sphere is simply connected, while the real projective plane has fundamental group Z2. The finite subgroups of SO(3), corresponding to the finite subgroups of O(2) and the symmetry groups of the platonic solids, do not act freely on S2, so the corresponding quotients are not 2-manifolds, just orbifolds.
 Eugenio Beltrami (1835-1899)
Eugenio Beltrami (1835-1899)
Hyperbolic geometry
See also: hyperbolic triangle and hyperbolic geometry Felix Klein (1849-1925)
Felix Klein (1849-1925)
 Henri Poincaré (1854-1912)
Henri Poincaré (1854-1912)
Non-Euclidean geometry[48] was first discussed in letters of Gauss, who made extensive computations at the turn of the nineteenth century which, although privately circulated, he decided not to put into print. In 1830 Lobachevsky and independently in 1832 Bolyai, the son of one Gauss' correspondents, published synthetic versions of this new geometry, for which they were severely criticized. However it was not until 1868 that Beltrami, followed by Klein in 1871 and Poincaré in 1882, gave concrete analytic models for what Klein dubbed hyperbolic geometry. The four models of 2-dimensional hyperbolic geometry that emerged were:
- the Beltrami-Klein model;
- the Poincaré disk;
- the Poincaré upper half-plane;
- the hyperboloid model of Wilhelm Killing in 3-dimensional Minkowski space.
The first model, based on a disk, has the advantage that geodesics are actually line segments (that is, intersections of Euclidean lines with the open unit disk).The last model has the advantage that it gives a construction which is completely parallel to that of the unit sphere in 3-dimensional Euclidean space. Because of their application in complex analysis and geometry, however, the models of Poincaré are the most widely used: they are interchangeable thanks to the Möbius transformations between the disk and the upper half-plane.
Let
be the Poincaré disk in the complex plane with Poincaré metric
In polar coordinates (r, θ) the metric is given by
The length of a curve γ:[a,b]
 D is given by the formula
D is given by the formulaThe group G = SU(1,1) given by
acts transitively by Möbius transformations on D and the stabilizer subgroup of 0 is the rotation group
The quotient group SU(1,1)/±I is the group of orientation-preserving isometries of D. Any two points z, w in D are joined by a unique geodesic, given by the portion of the circle or straight line passing through z and w and orthogonal to the boundary circle. The distance between z and w is given by
In particular d(0,r) = 2 tanh−1 r and c(t) = tanh t/2 is the geodesic through 0 along the real axis, parametrized by arclength.
The topology defined by this metric is equivalent to the usual Euclidean topology, although as a metric space (D,d) is complete.
A hyperbolic triangle is a geodesic triangle for this metric: any three points in D are vertices of a hyperbolic triangle. If the sides have length a, b, c with corresponding angles α, β, γ, then the hyperbolic cosine rule states that
The area of the hyperbolic triangle is given by[49]
- Area = π – α – β – γ.
The unit disk and the upper half-plane
are conformally equivalent by the Möbius transformations
Under this correspondence the action of SL(2,R) by Möbius transformations on H corresponds to that of SU(1,1) on D. The metric on H becomes
Since lines or circles are preserved under Möbius transformations, geodesics are again described by lines or circles orthogonal to the real axis.
The unit disk with the Poincaré metric is the unique simply connected oriented 2-dimensional Riemannian manifold with constant curvature -1. Any oriented closed surface M with this property has D as its universal covering space. Its fundamental group can be identified with a torsion-free concompact subgroup Γ of SU(1,1), in such a way that
In this case Γ is a finitely presented group. The generators and relations are encoded in a geodesically convex fundamental geodesic polygon in D (or H) corresponding geometrically to closed geodesics on M.
Examples.
- the Bolza surface of genus 2;
- the Klein quartic of genus 3;
- the Macbeath surface of genus 7;
- the First Hurwitz triplet of genus 14.
Uniformization
Given an oriented closed surface M with Gaussian curvature K, the metric on M can be changed conformally by scaling it by a factor e2u. The new Gaussian curvature K' is then given by
where Δ is the Laplacian for the original metric. Thus to show that a given surface is conformally equivalent to a metric with constant curvature K' it suffices to solve the following variant of Liouville's equation:
When M has Euler characteristic 0, so is diffeomorphic to a torus, K' = 0, so this amounts to solving
- Δu = K(x).
By standard elliptic theory, this is possible because the integral of K over M is zero, by the Gauss-Bonnet theorem.[50]
When M has negative Euler characteristic, K' = -1, so the equation to be solved is:
- Δu = − e2u + K(x).
Using the continuity of the exponential map on Sobolev space due to Neil Trudinger, this non-linear equation can always be solved.[51]
Finally in the case of the 2-sphere, K' = 1 and the equation becomes:
- Δu = e2u + K(x).
So far this non-linear equation has not been analysed directly, although classical results such as the Riemann-Roch theorem imply that it always has a solution. The method of Ricci flow, developed by Richard Hamilton, gives another proof of existence based on non-linear partial differential equations to prove existence.[52] In fact the Ricci flow on conformal metrics on S2 is defined on functions u(x, t) by
- ut = 4π − K'(x,t) = 4π − e − 2u(K(x) − Δu).
After finite time, Chow showed that K' becomes positive; previous results of Hamilton could then be used to show that K' converges to +1.[53]
A simple proof using only elliptic operators discovered in 1988 can be found in Ding (2001). Let G be the Green's function on S2 satisfying ΔG = 1 + 4πδP, where δP is the point measure at a fixed point P of S2. The equation Δv = 2K – 2, has a smooth solution v, because the right hand side has integral 0 by the Gauss-Bonnet theorem. Thus φ = 2G + v satisfies Δφ = 2K away from P. It follows that g1 = eφg is a complete metric of constant curvature 0 on the complement of P, which is therefore isometric to the plane. Composing with stereographic projection, it follows that there is a smooth function u such that e2ug has Gaussian curvature +1 on the complement of P. The function u automatically extends to a smooth function on the whole of S2.[54]
Surfaces of non-positive curvature
In a region where the curvature of the surface satisfies K≤0, geodesic triangles satisfy the CAT(0) inequalities of comparison geometry, studied by Cartan, Alexandrov and Toponogov, and considered later from a different point of view by Bruhat and Tits; thanks to the vision of Gromov, this characterisation of non-positive curvature in terms of the underlying metric space has had a profound impact on modern geometry and in particular geometric group theory. Many results known for smooth surfaces and their geodesics, such as Birkhoff's method of constructing geodesics by his curve-shortening process or van Mangoldt and Hadamard's theorem that a simply connected surface of non-positive curvature is homeomorphic to the plane, are equally valid in this more general setting.
Alexandrov's comparison inequality
 The median in the comparison triangle is always longer than the actual median.
The median in the comparison triangle is always longer than the actual median.
The simplest form of the comparison inequality, first proved for surfaces by Alexandrov around 1940, states that
The distance between a vertex of a geodesic triangle and the midpoint of the opposite side is always less than the corresponding distance in the comparison triangle in the plane with the same side-lengths.
The inequality follows from the fact that if c(t) describes a geodesic parametrised by arclength and a is a fixed point, then
- f(t) = d(a,c(t))2 − t2
is a convex function, i.e.
Taking geodesic polar coordinates with origin at a so that ||c(t)|| = r(t), convexity is equivalent to
Changing to normal coordinates u, v at c(t), this inequality becomes
- u2 + H − 1 Hr v2 ≥ 1,
where (u,v) corresponds to the unit vector
 . This follows from the inequality Hr ≥ H, a consequence of the non-negativity of the derivative of the Wronskian of H and r from Sturm–Liouville theory.[55]
. This follows from the inequality Hr ≥ H, a consequence of the non-negativity of the derivative of the Wronskian of H and r from Sturm–Liouville theory.[55]Existence of geodesics
On a complete curved surface any two points can be joined by a geodesic. This is a special case of the Hopf-Rinow theorem, which also applies in higher dimensions. The completeness assumption is automatically fulfilled for a surface which is embedded as a closed subset of Euclidean space. However, it is no longer fulfilled if, for example, we remove an isolated point from a surface. For example, the complement of the origin in the Euclidean plane is an example of a non-complete surface; in this example two points which are diametrically opposite across the origin cannot be joined by a geodesic without leaving the punctured plan).
Von Mangoldt-Hadamard theorem
For closed surfaces of non-positive curvature, von Mangoldt (1881) and Hadamard (1898) proved that the exponential map at a point is a covering map, so that the universal covering space of the manifold is E². This result was generalised to higher dimensions by Cartan and is usually referred to in this form as the Cartan–Hadamard theorem. For surfaces, this result follows from three important facts:[56]
- The exponential map has non-zero Jacobian everywhere for non-positively curved surfaces, a consequence of the non-vanishing of Hr.
- Every geodesic is infinitely extendible, a result known as the Hopf-Rinow theorem for n-dimensional manifolds. In two dimensions, if a geodesic tended at infinity towards a point x, a closed disc D centred on a nearby point y with x removed would be contractible to y along geodesics, a topological impossibility.
- Every two points in a homotopy class are connected by a unique geodesic (see above).
Riemannian connection and parallel transport
Main article: Riemannian connection on a surface Tullio Levi-Civita (1873-1941)
Tullio Levi-Civita (1873-1941)
The classical approach of Gauss to the differential geometry of surfaces was the standard elementary approach[57] which predated the emergence of the concepts of Riemannian manifold initiated by Bernhard Riemann in the mid-nineteenth century and of connection developed by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early twentieth century. The notion of connection, covariant derivative and parallel transport gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes.[58] The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.[59]
Covariant derivative
Connections on a surface can be defined from various equivalent but equally important points of view. The Riemannian connection or Levi-Civita connection[6] is perhaps most easily understood in terms of lifting vector fields, considered as first order differential operators acting on functions on the manifold, to differential operators on the tangent bundle or frame bundle. In the case of an embedded surface, the lift to an operator on vector fields, called the covariant derivative, is very simply described in terms of orthogonal projection. Indeed a vector field on a surface embedded in
 can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci and Levi-Civita realised at the turn of the twentieth century, this process depends only on the metric and can be locally expressed in terms of the Christoffel symbols.
can be regarded as a function from the surface into R3. Another vector field act as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci and Levi-Civita realised at the turn of the twentieth century, this process depends only on the metric and can be locally expressed in terms of the Christoffel symbols.Parallel transport
Parallel transport of tangent vectors along a curve in the surface was the next major advance in the subject, due to Levi-Civita.[6] It is related to the earlier notion of covariant derivative, because it is the monodromy of the ordinary differential equation on the curve defined by the covariant derivative with respect to the velocity vector of the curve. Parallel transport along geodesics, the "straight lines" of the surface, can also easily be described directly. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a constant angle with the velocity vector of the geodesic. For a general curve, this process has to be modified using the geodesic curvature, which measures how far the curve departs from being a geodesic.[5]
A vector field v(t) along a unit speed curve c(t), with geodesic curvature kg(t), is said to be parallel along the curve if
- it has constant length
- the angle θ(t) that it makes with the velocity vector
 satisfies
satisfies
This recaptures the rule for parallel transport along a geodesic or piecewise geodesic curve, because in that case kg = 0, so that the angle θ(t) should remain constant on any geodesic segment. The existence of parallel transport follows because θ(t) can be computed as the integral of the geodesic curvature. Since it therefore depends continuously on the L2 norm of kg, it follows that parallel transport for an arbitrary curve can be obtained as the limit of the parallel transport on approximating piecewise geodesic curves.[60]
The connection can thus be described in terms of lifting paths in the manifold to paths in the tangent or orthonormal frame bundle, thus formalising the classical theory of the "moving frame", favoured by French authors.[61] Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly at an infinitesimal level in terms of Lie brackets of lifted vector fields.
 Élie Cartan (1869-1951)
Élie Cartan (1869-1951)
Connection 1-form
The approach of Cartan and Weyl, using connection 1-forms on the frame bundle of M, gives a third way to understand the Riemannian connection. They noticed that parallel transport dictates that a path in the surface be lifted to a path in the frame bundle so that its tangent vectors lie in a special subspace of codimension one in the three-dimensional tangent space of the frame bundle. The projection onto this subspace is defined by a differential 1-form on the orthonormal frame bundle, the connection form. This enabled the curvature properties of the surface to be encoded in differential forms on the frame bundle and formulas involving their exterior derivatives.
This approach is particularly simple for an embedded surface. Thanks to a result of Kobayashi (1956), the connection 1-form on a surface embedded in Euclidean space E3 is just the pullback under the Gauss map of the connection 1-form on S2.[62] Using the identification of S2 with the homogeneous space SO(3)/SO(2), the connection 1-form is just a component of the Maurer-Cartan 1-form on SO(3).[63]
Global differential geometry of surfaces
Although the characterisation of curvature involves only the local geometry of a surface, there are important global aspects such as the Gauss-Bonnet theorem, the uniformization theorem, the von Mangoldt-Hadamard theorem, and the embeddability theorem. There are other important aspects of the global geometry of surfaces.[64] These include:
- Injectivity radius, defined as the largest r such that two points at a distance less than r are joined by a unique geodesic. Wilhelm Klingenberg proved in 1959 that the injectivity radius of a closed surface is bounded below by the minimum of
 and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by δ; in other words a geodesic realising the metric distance between two points cannot have length greater than δ.
and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by δ; in other words a geodesic realising the metric distance between two points cannot have length greater than δ.
- Rigidity. In 1927 Cohn-Vossen proved that two ovaloids – closed surfaces with positive Gaussian curvature – that are isometric are necessarily congruent by an isometry of E3. Moreover a closed embedded surface with positive Gaussian curvature and constant mean curvature is necessarily a sphere; likewise a closed embedded curvature of constant Gaussian curvature must be a sphere (Liebmann 1899). Heinz Hopf showed in 1950 that a closed embedded surface with constant mean curvature and genus 0, i.e. homeomorphic to a sphere, is necessarily a sphere; five years later Alexandrov removed the topological assumption. In the 1980s, Wente constructed immersed tori of constant mean curvature in Euclidean 3-space.
- Carathéodory conjecture: This conjecture states that a closed convex three times differentiable surface admits at least two umbilic points. The first work on this conjecture was in 1924 by Hans Hamburger, who noted that it follows from the following stronger claim : the half-integer valued index of the principal curvature foliation of an isolated umbilic is at most one. The contribution of Hamburger and those of subsequent authors to proving this local conjecture are inconclusive.
- Zero Gaussian curvature: a complete surface in E3 with zero Gaussian curvature must be a cylinder or a plane.
- Hilbert's theorem (1901): no complete surface with constant negative curvature can be immersed isometrically in E3.
- The Willmore conjecture. This conjecture states that the integral of the square of the mean curvature of a torus immersed in E3 should be bounded below by 2 π2. The conjecture has been proved for large classes of torus immersions. It is also known that the integral is a conformal invariant.
- Isoperimetric inequalities. In 1939 Schmidt proved that the classical isoperimetric inequality for curves in the Euclidean plane is also valid on the sphere or in the hyperbolic plane: namely he showed that among all closed curves bounding a domain of fixed area, the perimeter is minimized by when the curve is a circle for the metric. In one dimension higher, it is known that among all closed surfaces in E3 arising as the boundary of a bounded domain of unit volume, the surface area is minimized for a Euclidean ball.
- Systolic inequalities for curves on surfaces. Given a closed surface, its systole is defined to be the smallest length of any non-contractible closed curve on the surface. In 1949 Loewner proved a torus inequality for metrics on the torus, namely that the area of the torus over the square of its systole is bounded below by
 , with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of 2/π also attained in the constant curvature case. For the Klein bottle, Blatter and Bavard later obtained a lower bound of
, with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of 2/π also attained in the constant curvature case. For the Klein bottle, Blatter and Bavard later obtained a lower bound of  . For a closed surface of genus g, Hebda and Burago showed that the ratio is bounded below by 1/2. Three years later Mikhail Gromov found a lower bound given by a constant times g1/2, although this is not optimal. Asymptotically sharp upper and lower bounds given by constants times g/(log g)2 are due to Gromov and Buser-Sarnak, and can be found in Katz (2007). There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesic. Gromov conjectured a lower bound of
. For a closed surface of genus g, Hebda and Burago showed that the ratio is bounded below by 1/2. Three years later Mikhail Gromov found a lower bound given by a constant times g1/2, although this is not optimal. Asymptotically sharp upper and lower bounds given by constants times g/(log g)2 are due to Gromov and Buser-Sarnak, and can be found in Katz (2007). There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesic. Gromov conjectured a lower bound of  in 1980: the best result so far is the lower bound of 1/8 obtained by Regina Rotman in 2006.[65]
in 1980: the best result so far is the lower bound of 1/8 obtained by Regina Rotman in 2006.[65]
Reading guide
One of the most comprehensive introductory surveys of the subject, charting the historical development from before Gauss to modern times, is by Berger (2004). Accounts of the classical theory are given in Eisenhart (2004), Kreyszig (1991) and Struik (1988); the more modern copiously illustrated undergraduate textbooks by Gray, Abbena & Salamon (2006), Pressley (2001) and Wilson (2008) might be found more accessible. An accessible account of the classical theory can be found in Hilbert & Cohn-Vossen (1952). More sophisticated graduate-level treatments using the Riemannian connection on a surface can be found in Singer & Thorpe (1967), do Carmo (1976) and O'Neill (1997).
See also
Notes
- ^ Euler 1760
- ^ Euler 1771
- ^ Gauss 1825-1827
- ^ This is the final position into which a rubber band stretched between two fixed points on the surface would fall.
- ^ a b c d Berger 2004
- ^ a b c d e f g h Eisenhart 2004, p. 123
- ^ Singer & Thorpe 1967, p. 223
- ^ do Carmo 1976, pp. 161–162
- ^ Eisenhart 2004, pp. 228–229
- ^ Eisenhart 2004, pp. 241–250; do Carmo 1976, pp. 188–197.
- ^ do Carmo 1976, p. 194.
- ^ Eisenhart 2004, pp. 61–65.
- ^ Eisenhart 2004, pp. 250–269; do Carmo 1976, pp. 197–213.
- ^ Douglas' solution is described in Courant (1950).
- ^ Eisenhart 2004, pp. 270–291; O'Neill, pp. 249–251; Hilbert & Cohn-Vossen 1952.
- ^ O'Neill, pp. 249–251; do Carmo, pp. 168–170; Gray, Abbena & Salamon 2006.
- ^ Stillwell 1996, pp. 1–5.
- ^ Wilson 2008.
- ^ Eisenhart 2004, pp. 114–115; Pressley 2001, pp. 123–124; Wilson 2008, pp. 123–124.
- ^ Eisenhart 2004, p. 156
- ^ O'Neill 1997, p. 257
- ^ do Carmo 1976, pp. 309–314
- ^ O'Neill 1997, pp. 195–216; do Carmo 1976, pp. 134–153; Singer & Thorpe 1967, pp. 216–224.
- ^ Gray, Abbena & Salamon 2006, p. 386.
- ^ Note that in some more recent texts the symmetric bilinear form on the right hand side is referred to as the second fundamental form; however, it does not in general correpond to the classically defined second fundamental form.
- ^ Gray, Abbena & Salamon 2006, p. 394.
- ^ Berger 2004; Wilson 2008; Milnor 1963.
- ^ Eisenhart 2002, p. 131; Berger 2004, p. 39; do Carmo 1976, p. 248; O'Neill 1997, p. 237
- ^ Han & Hong 2006
- ^ Eisenhart 2004; Taylor 1996a, Appendix C.
- ^ Eisenhart 2004; Berger 2004.
- ^ doCarmo 1976, p. 357
- ^ Milnor 1963
- ^ Wilson 2008
- ^ O'Neill 1997, p. 395
- ^ Helgason 1978, p. 92
- ^ O'Niell 1997, p. 286
- ^ do Carmo 1976, p. 227
- ^ Osserman 2002, pp. 31–32
- ^ Singer & Thorpe 1967; Garsia, Adriano M. (1961), "An imbedding of closed Riemann surfaces in Euclidean space", Comment. Math. Helv. 35: 93–110, doi:10.1007/BF02567009
- ^ Imayoshi & Taniguchi 1992, pp. 47–49
- ^ Berger 1977; Taylor 1996.
- ^ Wilson 2008, pp. 1–23, Chapter I, Euclidean geometry.
- ^ do Carmo 1976.
- ^ Wilson 2008, pp. 25–49, Chapter II, Spherical geometry.
- ^ Wilson 2008, Chapter 2.
- ^ Eisenhart 2004, p. 110.
- ^ Stillwell 1990; Bonola, Carslaw & Enriques 1955.
- ^ Wilson 2008, Chapter 5.
- ^ Taylor 1996b, p. 107; Berger 1977, pp. 341–343.
- ^ Berger 1977, pp. 222–225; Taylor 1996b, pp. 101–108.
- ^ Chow 1991; Taylor 1996b.
- ^ Chen, Lu & Tian (2006) pointed out a missing step in the approach of Hamilton and Chow.
- ^ This follows by an argument involving a theorem of Sacks & Uhlenbeck (1981) on removable singularities of harmonic maps of finite energy.
- ^ Berger 2004; Jost, Jürgen (1997), Nonpositive curvature: geometric and analytic aspects, Lectures in Mathematics, ETH Zurich, Birkhäuser, ISBN 0817657363
- ^ do Carmo 1976; Berger 2004.
- ^ Eisenhart 2004; Kreyszig 1991; Berger 2004; Wilson 2008.
- ^ Kobayashi & Nomizu 1969, Chapter XII.
- ^ do Carmo 1976; O'Neill 1997; Singer & Thorpe 1967.
- ^ Arnold 1989, pp. 301–306, Appendix I.; Berger 2004, pp. 263–264.
- ^ Darboux 1887,1889,1896
- ^ Kobayashi & Nomizu 1969
- ^ Ivey & Landsberg 2003.
- ^ Berger 2004, pp. 145–161; do Carmo 1976; Chern 1967; Hopf 1989.
- ^ Rotman, R. (2006) "The length of a shortest closed geodesic and the area of a 2-dimensional sphere," Proc. Amer. Math. Soc. 134: 3041-3047. Previous lower bounds had been obtained by Croke, Rotman-Nabutovsky and Sabourau.
References
- Aleksandrov, A.D.; Zalgaller, V.A. (1967), Instrinsic Geometry of Surfaces, Translations of Mathematical Monographs, 15, American Mathematical Society
- Arnold, V.I. (1989), Mathematical methods of classical mechanics., Graduate Texts in Mathematics, 60 (2nd ed.), New York: Springer-Verlag, ISBN 0387903143; translated from the Russian by K. Vogtmann and A. Weinstein.
- Berger, Marcel (2004), A Panoramic View of Riemannian Geometry, Springer-Verlag, ISBN 3540653171
- Berger, Melvyn S. (1977), Nonlinearity and Functional Analysis, Academic Press, ISBN 0120903504
- Bonola, Roberto; Carslaw, H. S.; Enriques, F. (1955), Non-Euclidean Geometry: A Critical and Historical Study of Its Development, Dover, ISBN 0486600270
- Cartan, Élie (1983), Geometry of Riemannian Spaces, Math Sci Press, ISBN 9780915692347, http://books.google.com/?id=-YvvVfQ7xz4C&printsec=frontcover&dq=geometry+of+riemannian+spaces+cartan; translated from 2nd edition of Leçons sur la géométrie des espaces de Riemann (1951) by James Glazebrook.
- Cartan, Élie (2001), Riemannian Geometry in an Orthogonal Frame (from lectures delivered by É Cartan at the Sorbonne in 1926-27), World Scientific, ISBN 981024746X, http://ebooks.worldscinet.com/mathematics/9789812799715/preserved-docs/9789812799715.pdf[dead link]; translated from Russian by V. V. Goldberg with a foreword by S. S. Chern.
- Chen, Xiuxiong; Lu, Peng; Tian, Gang (2006), "A note on uniformization of Riemann surfaces by Ricci flow", Proc. AMS. 134 (11): 3391–3393, doi:10.1090/S0002-9939-06-08360-2
- Chern, S. S. (1967), Curves and Surfaces in Euclidean Spaces, MAA Studies in Mathematics, Mathematical Association of America
- Chow, B. (1991), "The Ricci flow on a 2-sphere", J. Diff. Geom. 33: 325–334
- Courant, Richard (1950), Dirichlet's Principle, Conformal Mapping and Minimal Surfaces, John Wiley & Sons, ISBN 0486445526
- Darboux, Gaston (1887,1889,1896), Leçons sur la théorie génerale des surfaces: Volume I, Volume II, Volume III, Volume IV, Gauthier-Villars
- Ding, W. (2001), "A proof of the uniformization theorem on S2", J. Partial Differential Equations 14: 247–250
- do Carmo, Manfredo P. (1976), Differential Geometry of Curves and Surfaces, Prentice-Hall, ISBN 0132125897
- Eisenhart, Luther P. (2004), A Treatise on the Differential Geometry of Curves and Surfaces, Dover, ISBN 0486438201 Full 1909 text (now out of copyright)
- Eisenhart, Luther P. (1947), An Introduction to Differential Geometry with Use of the Tensor Calculus, Princeton Mathematical Series, 3, Princeton University Press, ISBN 1443722936
- Euler, Leonard (1760), "Recherches sur la courbure des surfaces", Memoires de l'academie des sciences de Berlin 16: 119–143, 1767, http://math.dartmouth.edu/~euler/pages/E333.html.
- 34, "De solidis quorum superficiem in planum explicare licet", published 1772.
- Gauss, Carl Friedrich (1825–1827), General Investigations of Curved Surfaces, New York: Raven Press (published 1965), ISBN 048644645X, http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABR1255 translated by A.M.Hiltebeitel and J.C.Morehead; "Disquisitiones generales circa superficies curvas", Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores Vol. VI (1827), pp. 99-146.
- Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves And Surfaces With Mathematica, CRC Press, ISBN 1584884487
- Han, Qing; Hong, Jia-Xing (2006), Isometric Embedding of Riemannian Manifolds in Euclidean Spaces, American Mathematical Society, ISBN 0821840711
- Helgason, Sigurdur (1978), Differential Geometry, Lie Groups, and Symmetric Spaces, Academic Press, New York, ISBN 0123384605
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8
- Hopf, Heinz (1989), Lectures on Differential Geometry in the Large, Lecture Notes in Mathematics, 1000, Springer-Verlag, ISBN 354051497X
- Imayoshi, Y.; Taniguchi, M. (1992), An Introduction to Techmüller spaces, Springer-Verlag, ISBN 0-387-70088-9
- Ivey, Thomas A.; Landsberg, J.M. (2003), Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems, Graduate Studies in Mathematics, 61, American Mathematical Society, ISBN 0821833758
- Jacobowitz, Howard (1972), "Local Isometric Embeddings of Surfaces into Euclidean Four Space", Indiana Univ. Math. J. 21 (3): 249–254, doi:10.1512/iumj.1971.21.21019, http://www.iumj.indiana.edu/IUMJ/FULLTEXT/1972/21/21019
- Katz, Mikhail G. (2007), Systolic geometry and topology, Mathematical Surveys and Monographs, 137, American Mathematical Society, ISBN 0821841777
- Kobayashi, Shoshichi (1956), "Induced connections and imbedded Riemannian space", Nagoya Math. J. 10: 15–25
- Kobayashi, Shoshichi (1957), "Theory of connections", Annali di Matematica Pura ed Applicata. Serie Quarta 43: 119–194, doi:10.1007/BF02411907,
- Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Foundations of differential geometry, Vol. I, Wiley Interscience, ISBN 0-470-49648-7
- Kobayashi, Shoshichi; Nomizu, Katsumi (1969), Foundations of differential geometry, Vol. II, Wiley Interscience, ISBN 0-470-49648-7
- Kreyszig, Erwin (1991), Differential Geometry, Dover, ISBN 0486667219
- Kühnel, Wolfgang (2006), Differential Geometry: Curves - Surfaces - Manifolds, American Mathematical Society, ISBN 0-8218-3988-8
- Levi-Civita, Tullio (1917), "Nozione di parallelismo in una varieta qualunque", Rend. Circ. Mat. Palermo 42: 173–205, doi:10.1007/BF03014898
- O'Neill, Barrett (1997), Elementary Differential Geometry, Academic Press, ISBN 0125267509
- Osserman, Robert (2002), A Survey of Minimal Surfaces, Dover, ISBN 0486495140
- Ian R. Porteous (2001) Geometric Differentiation: for the intelligence of curves and surfaces, Cambridge University Press ISBN 0-521-00264-8 .
- Poznjak, E.G. (1973), "Isometric imbedding of two-dimensional Riemannian metrics in Euclidean spaces", Russian Math. Surveys 28 (4): 47–77, doi:10.1070/RM1973v028n04ABEH001591
- Pressley, Andrew (2001), Elementary Differential Geometry, Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 1852331526
- Sacks, J.; Uhlenbeck, Karen (1981), "The existence of minimal immersions of 2-spheres", Ann. Of Math. 112 (1): 1–24, doi:10.2307/1971131, JSTOR 1971131
- Singer, Isadore M.; Thorpe, John A. (1967), Lecture Notes on Elementary Topology and Geometry, Springer-Verlag, ISBN 0387902023
- Stillwell, John (1996), Sources of Hyperbolic Geometry, American Mathematical Society, ISBN 0821805584
- Struik, Dirk Jan (1988), Lectures on classical differential geometry: Second Edition, Dover, ISBN 0-486-65609-8
- Taylor, Michael E. (1996a), Partial Differential Equations II: Qualitative Studies of Linear Equations, Springer-Verlag, ISBN 1441970517
- Taylor, Michael E. (1996b), Partial Differential Equations III: Nonlinear equations, Springer-Verlag, ISBN 1441970487
- Toponogov, Victor A. (2005), Differential Geometry of Curves and Surfaces: A Concise Guide, Springer-Verlag, ISBN 0817643842
- Valiron, Georges (1986), The Classical Differential Geometry of Curves and Surfaces, Math Sci Press, ISBN 0915692392 Full text of book
- Wilson, Pelham (2008), Curved Space: From Classical Geometries to Elementary Differential Geometry, Cambridge University Press, ISBN 978-0-521-71390-0
Various notions of curvature defined in differential geometry Differential geometry of curves Differential geometry of surfaces Riemannian geometry Curvature of connections Categories:
Wikimedia Foundation. 2010.
















![K=-{\beta^2\over (s-\alpha)^2 +\beta^2} ,\,\, K_m=-{r[(s-\alpha)^2 +\beta^2)] +\beta_t(s-\alpha) + \beta\alpha_t\over
[(s-\alpha)^2 +\beta^2]^{3/2}}.](1/a217f826cfd4d6b10ffc5e5426cda324.png)
















![K=-{1\over 2H} \left[\partial_x(G_x/H) +\partial_y(E_y/H)\right]](0/34097f30ed667948d306ccc99221b6cb.png)