- Orbifold notation
-
In geometry, orbifold notation (or orbifold signature) is a system, invented by William Thurston and popularized by the mathematician John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it describes the orbifold obtained by taking the quotient of Euclidean space by the group under consideration.
Groups representable in this notation include the point groups on the sphere (S2), the frieze groups and wallpaper groups of the Euclidean plane (E2), and their analogues on the hyperbolic plane (H2).
Contents
Definition of the notation
The following types of Euclidean transformation can occur in a group described by orbifold notation:
- reflection through a line (or plane)
- translation by a vector
- rotation of finite order around a point
- infinite rotation around a line in 3-space
- glide-reflection, i.e. reflection followed by translation
All translations which occur are assumed to form a discrete subgroup of the group symmetries being described.
Each group is denoted in orbifold notation by a finite string made up from the following symbols:
- positive integers

- the infinity symbol,

- the asterisk, *
- the symbol o, which is called a wonder (Older documents show this as a solid circle)
- the symbol x, which is called a miracle (Older documents show this as an open circle)
A string written in boldface represents a group of symmetries of Euclidean 3-space. A string not written in boldface represents a group of symmetries of the Euclidean plane, which is assumed to contain two independent translations.
Each symbol corresponds to a distinct transformation:
- an integer n to the left of an asterisk indicates a rotation of order n around a point
- an integer n to the right of an asterisk indicates a transformation of order 2n which rotates around a point and reflects through a line (or plane)
- an x indicates a glide reflection
- the symbol
 indicates infinite rotational symmetry around a line; it can only occur for bold face groups. By abuse of language, we might say that such a group is a subgroup of symmetries of the Euclidean plane with only one independent translation. The frieze groups occur in this way.
indicates infinite rotational symmetry around a line; it can only occur for bold face groups. By abuse of language, we might say that such a group is a subgroup of symmetries of the Euclidean plane with only one independent translation. The frieze groups occur in this way. - the exceptional symbol o indicates that there are precisely two linearly independent translations.
Chirality and achirality
An object is chiral if its symmetry group contains no reflections; otherwise it is called achiral. The corresponding orbifold is orientable in the chiral case and non-orientable otherwise.
The Euler characteristic and the order
The Euler characteristic of an orbifold can be read from its Conway symbol, as follows. Each feature has a value:
- n without or before an asterisk counts as

- n after an asterisk counts as

- asterisk and x count as 1
- o counts as 2
Subtracting the sum of these values from 2 gives the Euler characteristic.
If the sum of the feature values is 2, the order is infinite, i.e., the notation represents a wallpaper group or a frieze group. Indeed, Conway's "Magic Theorem" indicates that the 17 wallpaper groups are exactly those with the sum of the feature values equal to 2. Otherwise, the order is 2 divided by the Euler characteristic.
Equal groups
The following groups are isomorphic:
- 1* and *11
- 22 and 221
- *22 and *221
- 2* and 2*1
This is because 1-fold rotation is the "empty" rotation.
Other objects

A perfect snowflake would have *66 symmetry,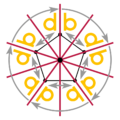
The pentagon has symmetry *55, the whole image with arrows 55.
The Flag of Hong Kong has 5 fold rotation symmetry, 55.The symmetry of a 2D object without translational symmetry can be described by the 3D symmetry type by adding a third dimension to the object which does not add or spoil symmetry. For example, for a 2D image we can consider a piece of carton with that image displayed on one side; the shape of the carton should be such that it does not spoil the symmetry, or it can be imagined to be infinite. Thus we have nn and *nn.
Similarly, a 1D image can be drawn horizontally on a piece of carton, with a provision to avoid additional symmetry with respect to the line of the image, e.g. by drawing a horizontal bar under the image. Thus the discrete symmetry groups in one dimension are 11, *11,
 and *
and * .
.Another way of constructing a 3D object from a 1D or 2D object for describing the symmetry is taking the Cartesian product of the object and an asymmetric 2D or 1D object, respectively.
Correspondence tables
Spherical
See also: List of spherical symmetry groups
Spherical Symmetry Groups: (n=3,4,..)[1] Orbifold
SignatureCoxeter Schönflies Hermann–Mauguin Order Polyhedral groups *532 [3,5] Ih 53m 120 532 [3,5]+ I 532 60 *432 [3,4] Oh m3m 48 432 [3,4]+ O 432 24 *332 [3,3] Td 43m 24 3*2 [3+,4] Th m3 24 332 [3,3]+ T 23 12 Dihedral and cyclic groups: n=3,4,5... *22n [2,n] Dnh n/mmm or 2nm2 4n 2*n [2+,2n] Dnd 2n2m or nm 4n 22n [2,n]+ Dn n2 2n *nn [n] Cnv nm 2n n* [2,n+] Cnh n/m or 2n 2n nx [2+,2n+] S2n 2n or n 2n nn [n]+ Cn n n Special cases *222 [2,2] D2h 2/mmm or 22m2 8 2*2 [2+,4] D2d 222m or 2m 8 222 [2,2]+ D2 22 4 *22 [2] C2v 2m 4 2* [2,2+] C2h 2/m or 22 4 2x [2+,4+] S4 22 or 2 4 22 [2]+ C2 2 2 *221 [1,2] D1h 1/mmm or 21m2 4 2*1 [2+,2] D1d 212m or 1m 4 221 [1,2]+ D1 12 2 *11 [ ] C1v 1m 2 1* [2,1+] C1h 1/m or 21 2 1x [2+,2+] S2 21 or 1 2 11 [ ]+ C1 1 1 Euclidean plane
See also: List of planar symmetry groups
Frieze groups
Frieze groups Notations Description Examples IUC Orbifold Coxeter Schönflies* p1 ∞∞ [∞,1]+ C∞ (hop): Translations only. This group is singly generated, with a generator being a translation by the smallest distance over which the pattern is periodic. Abstract group: Z, the group of integers under addition. 
p11g ∞x [∞+,2+] S∞ (step): Glide-reflections and translations. This group is generated by a glide reflection, with translations being obtained by combining two glide reflections. Abstract group: Z p11m ∞* [∞+,2] C∞h (jump): Translations, the reflection in the horizontal axis and glide reflections. This group is generated by a translation and the reflection in the horizontal axis. Abstract group: Z × Z2 p1m1 *∞∞ [∞,1] C∞v (sidle): Translations and reflections across certain vertical lines. The group is the same as the non-trivial group in the one-dimensional case; it is generated by a translation and a reflection in the vertical axis. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with Z2. Abstract group: Dih∞, the infinite dihedral group. p2 22∞ [∞,2]+ D∞ (spinning hop): Translations and 180° rotations. The group is generated by a translation and a 180° rotation. Abstract group: Dih∞ p2mg 2*∞ [∞,2+] D∞d (spinning sidle): Reflections across certain vertical lines, glide reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and either a rotation or a vertical reflection. Abstract group: Abstract group: Dih∞ p2mm *22∞ [∞,2] D∞h (spinning jump): Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. Abstract group: Dih∞ × Z2 - *Schönflies's point group notation is extended here as infinite cases of the equivalent dihedral points symmetries
Wallpaper groups
17 wallpaper groups[2] Orbifold
SignatureCoxeter Hermann–Mauguin Speiser
NiggliPolya
GuggenheinFejes Toth
Cadwell*632 [6,3] p6m C(I)6v D6 W16 632 [6,3]+ p6 C(I)6 C6 W6 *442 [4,4] p4m C(I)4 D*4 W14 4*2 [4+,4] p4g CII4v Do4 W24 442 [4,4]+ p4 C(I)4 C4 W4 *333 [3[3]] p3m1 CII3v D*3 W13 3*3 [6,3+] p31m CI3v Do4 W23 333 [3[3]]+ p3 CI3 C3 W3 *2222 [∞,2,∞] pmm CI2v D2kkkk W22 2*22 [∞,2+,∞] cmm CIV2v D2kgkg W12 22* [(∞,2)+,∞] pmg CIII2v D2kkgg W32 22x [∞+,2+,∞+] pgg CII2v D2gggg W42 2222 [∞,2,∞]+ p2 C(I)2 C2 W2 ** [∞,2,∞+] pm CIs D1kk W21 *x [∞,2+,∞+] cm CIIIs D1kg W11 xx [(∞,2)+,∞+] pg CII2 D1gg W31 o [∞+,2,∞+] p1 C(I)1 C1 W1 Hyperbolic plane
A first few hyperbolic groups, ordered by their orbifold characteristic are:
Hyperbolic Symmetry Groups[3] (-1/char) Orbifolds Coxeter (84) *237 [7,3] (48) *238 [8,3] (42) 237 [7,3]+ (40) *245 [5,4] (24) *2.3.12, *246, *334, 3*4, 238 [12,3], [6,4], [(4,3,3)], [8,3]+ (20) *2.3.15, *255, 5*2, 245 [15,3], [5,5], [5+,4], [5,4]+ (18+2/3) *247 [7,4] (18) *2.3.18, 239 [18,3], [9,3]+ (16) *2.3.24, *248 [24,3], [8,4] (15) *2.3.30, *256, *335, 3*5, 2.3.10 [30,3], [6,5], [(5,3,3)], [3+,10], [10,3]+ (14+2/5) *2.3.36, *249 [36,3], [9,4] (13+1/3) *2.3.60, *2.4.10 [60,3], [10,4] (13+1/5) *2.3.66, 2.3.11 [66,3], [11,3]+ (12+8/11) *2.3.105, *257 [105,3], [7,5] (12+4/7) *2.3.132, *2.4.11 ... *23∞, *2.4.12, *266, 6*2 [132,3], [11,4], ..., [∞,3], [12,4], [6,6], [6+,4] (12) *336, 3*6, *344, 4*3, *2223, 2*23, 2.3.12, 246, 334 [(6,3,3)], [3+,12], [(4,4,3)], [4+,6], ... [12,3]+, [6,4]+ [(4,3,3)]+ ... See also
- Fibrifold notation - an extension of orbifold notation for 3d space groups
References
- John H. Conway, Olaf Delgado Friedrichs, Daniel H. Huson, and William P. Thurston. On Three-dimensional Orbifolds and Space Groups. Contributions to Algebra and Geometry, 42(2):475-507, 2001.
- J. H. Conway, D. H. Huson. The Orbifold Notation for Two-Dimensional Groups. Structural Chemistry, 13 (3-4): 247-257, August 2002.
- J. H. Conway (1992). "The Orbifold Notation for Surface Groups". In: M. W. Liebeck and J. Saxl (eds.), Groups, Combinatorics and Geometry, Proceedings of the L.M.S. Durham Symposium, July 5–15, Durham, UK, 1990; London Math. Soc. Lecture Notes Series 165. Cambridge University Press, Cambridge. pp. 438–447
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
- A field guide to the orbifolds (Notes from class on "Geometry and the Imagination" in Minneapolis, with John Conway, Peter Doyle, Jane Gilman and Bill Thurston, on June 17-28, 1991. See also PDF, 2006)
- 2DTiler Software for visualizing two-dimensional tilings of the plane and editing their symmetry groups in orbifold notation
Categories:- Group theory
- Generalized manifolds
- Mathematical notation
Wikimedia Foundation. 2010.



