- Subgroup
-
This article is about the mathematical conceptFor the galaxy-related concept, see Galaxy subgroup.
Concepts in group theory category of groups subgroups, normal subgroups group homomorphisms, kernel, image, quotient direct product, direct sum semidirect product, wreath product Types of groups simple, finite, infinite discrete, continuous multiplicative, additive cyclic, abelian, dihedral nilpotent, solvable list of group theory topics glossary of group theory In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H. This is usually represented notationally by H ≤ G, read as "H is a subgroup of G".
A proper subgroup of a group G is a subgroup H which is a proper subset of G (i.e. H ≠ G). The trivial subgroup of any group is the subgroup {e} consisting of just the identity element. If H is a subgroup of G, then G is sometimes called an overgroup of H.
The same definitions apply more generally when G is an arbitrary semigroup, but this article will only deal with subgroups of groups. The group G is sometimes denoted by the ordered pair (G,*), usually to emphasize the operation * when G carries multiple algebraic or other structures.
This article will write ab for a*b, as is usual.
Contents
Basic properties of subgroups
- A subset H of the group G is a subgroup of G if and only if it is nonempty and closed under products and inverses. (The closure conditions mean the following: whenever a and b are in H, then ab and a−1 are also in H. These two conditions can be combined into one equivalent condition: whenever a and b are in H, then ab−1 is also in H.) In the case that H is finite, then H is a subgroup if and only if H is closed under products. (In this case, every element a of H generates a finite cyclic subgroup of H, and the inverse of a is then a−1 = an − 1, where n is the order of a.)
- The above condition can be stated in terms of a homomorphism; that is, H is a subgroup of a group G if and only if H is a subset of G and there is an inclusion homomorphism (i.e., i(a) = a for every a) from H to G.
- The identity of a subgroup is the identity of the group: if G is a group with identity eG, and H is a subgroup of G with identity eH, then eH = eG.
- The inverse of an element in a subgroup is the inverse of the element in the group: if H is a subgroup of a group G, and a and b are elements of H such that ab = ba = eH, then ab = ba = eG.
- The intersection of subgroups A and B is again a subgroup.[1] The union of subgroups A and B is a subgroup if and only if either A or B contains the other, since for example 2 and 3 are in the union of 2Z and 3Z but their sum 5 is not. Another example is the union of the x-axis and the y-axis in the plane (with the addition operation); each of these objects is a subgroup but their union is not. This also serves as an example of two subgroups, whose intersection is precisely the identity.
- If S is a subset of G, then there exists a minimum subgroup containing S, which can be found by taking the intersection of all of subgroups containing S; it is denoted by <S> and is said to be the subgroup generated by S. An element of G is in <S> if and only if it is a finite product of elements of S and their inverses.
- Every element a of a group G generates the cyclic subgroup <a>. If <a> is isomorphic to Z/nZ for some positive integer n, then n is the smallest positive integer for which an = e, and n is called the order of a. If <a> is isomorphic to Z, then a is said to have infinite order.
- The subgroups of any given group form a complete lattice under inclusion, called the lattice of subgroups. (While the infimum here is the usual set-theoretic intersection, the supremum of a set of subgroups is the subgroup generated by the set-theoretic union of the subgroups, not the set-theoretic union itself.) If e is the identity of G, then the trivial group {e} is the minimum subgroup of G, while the maximum subgroup is the group G itself.
Cosets and Lagrange's theorem
Given a subgroup H and some a in G, we define the left coset aH = {ah : h in H}. Because a is invertible, the map φ : H → aH given by φ(h) = ah is a bijection. Furthermore, every element of G is contained in precisely one left coset of H; the left cosets are the equivalence classes corresponding to the equivalence relation a1 ~ a2 if and only if a1−1a2 is in H. The number of left cosets of H is called the index of H in G and is denoted by [G : H].
Lagrange's theorem states that for a finite group G and a subgroup H,
where |G| and |H| denote the orders of G and H, respectively. In particular, the order of every subgroup of G (and the order of every element of G) must be a divisor of |G|.
Right cosets are defined analogously: Ha = {ha : h in H}. They are also the equivalence classes for a suitable equivalence relation and their number is equal to [G : H].
If aH = Ha for every a in G, then H is said to be a normal subgroup. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if p is the lowest prime dividing the order of a finite group G, then any subgroup of index p (if such exists) is normal.
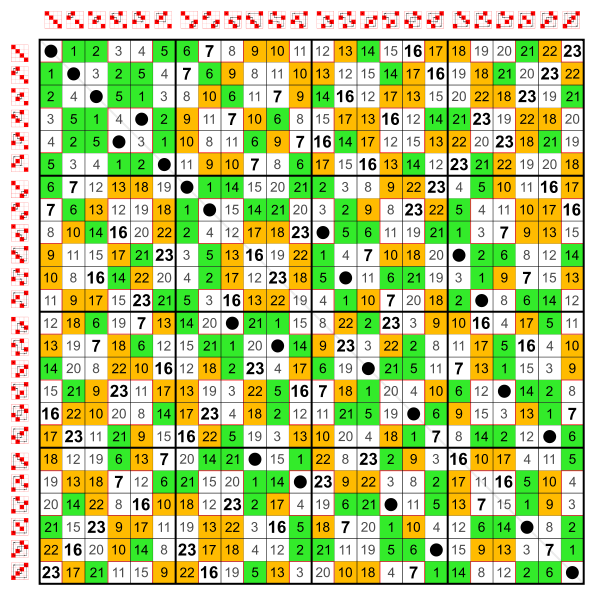
Example: Subgroups of Z8
Let G be the cyclic group Z8 whose elements are
and whose group operation is addition modulo eight. Its Cayley table is
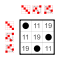
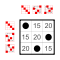
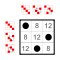
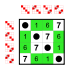
+ 0 2 4 6 1 3 5 7 0 0 2 4 6 1 3 5 7 2 2 4 6 0 3 5 7 1 4 4 6 0 2 5 7 1 3 6 6 0 2 4 7 1 3 5 1 1 3 5 7 2 4 6 0 3 3 5 7 1 4 6 0 2 5 5 7 1 3 6 0 2 4 7 7 1 3 5 0 2 4 6 This group has a pair of nontrivial subgroups: J={0,4} and H={0,2,4,6}, where J is also a subgroup of H. The Cayley table for H is the top-left quadrant of the Cayley table for G. The group G is cyclic, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.
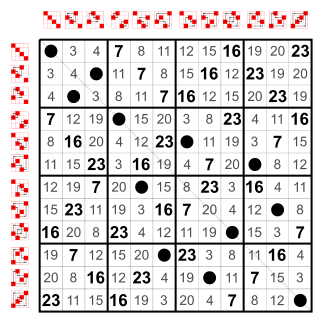
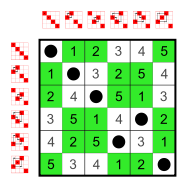
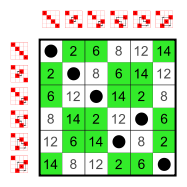
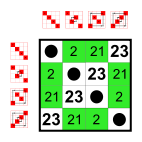
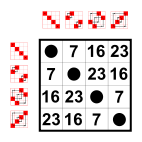
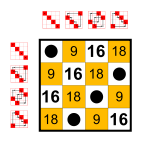
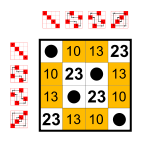
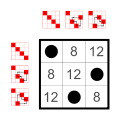
Example: Subgroups of S4
Every group has as many small subgroups as neutral elements on the main diagonal:
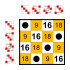
The trivial group and two-element groups Z2. These small subgroups are not counted in the following list.12 elements
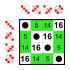
8 elements
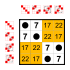
6 elements
4 elements
 Cyclic group Z4
Cyclic group Z4
3 elements
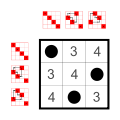 Cyclic group Z3
Cyclic group Z3
See also
- Cartan subgroup
- Fitting subgroup
- Stable subgroup
Notes
- ^ Jacobson (2009), p. 41
References
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
Categories:- Group theory
- Subgroup properties
Wikimedia Foundation. 2010.

![[ G : H ] = { |G| \over |H| }](8/398de907f3262d1d9c0d0121eaa87c20.png)