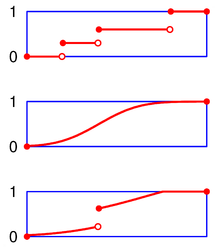
- Càdlàg
-
In mathematics, a càdlàg (French "continue à droite, limite à gauche"), RCLL (“right continuous with left limits”), or corlol (“continuous on (the) right, limit on (the) left”) function is a function defined on the real numbers (or a subset of them) that is everywhere right-continuous and has left limits everywhere. Càdlàg functions are important in the study of stochastic processes that admit (or even require) jumps, unlike Brownian motion, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.
Two related terms are càglàd, standing for "continue à gauche, limite à droite", the left-right reversal of càdlàg, and càllàl for"continue à l'un, limite à l’autre" (continuous on one side, limit on the other side), for a function which is interchangeably either càdlàg or càglàd at each point of the domain.
Contents
Definition
Let (M, d) be a metric space, and let E ⊆ R. A function ƒ: E → M is called a càdlàg function if, for every t ∈ E,
- the left limit ƒ(t−) := lims↑t ƒ(s) exists; and
- the right limit ƒ(t+) := lims↓t ƒ(s) exists and equals ƒ(t).
That is, ƒ is right-continuous with left limits.
Examples
- All continuous functions are càdlàg functions.
- As a consequence of their definition, all cumulative distribution functions are càdlàg functions.
- The right derivative f+' of any convex function f defined on an open interval, is an increasing cadlag function.
Skorokhod space
The set of all càdlàg functions from E to M is often denoted by D(E; M) (or simply D) and is called Skorokhod space after the Ukrainian mathematician Anatoliy Skorokhod. Skorokhod space can be assigned a topology that, intuitively allows us to"wiggle space and time a bit" (whereas the traditional topology of uniform convergence only allows us to "wiggle space a bit"). For simplicity, take E = [0, T] and M = Rn — see Billingsley for a more general construction.
We must first define an analogue of the modulus of continuity, ϖ′ƒ(δ). For any F ⊆ E, set
and, for δ > 0, define the càdlàg modulus to be
where the infimum runs over all partitions Π = {0 = t0 < t1 < … < tk = T}, k ∈ N, with mini (ti − ti−1) > δ. This definition makes sense for non-càdlàg ƒ (just as the usual modulus of continuity makes sense for discontinuous functions) and it can be shown that ƒ is càdlàg if and only if ϖ′ƒ(δ) → 0 as δ → 0.
Now let Λ denote the set of all strictly increasing, continuous bijections from E to itself (these are "wiggles in time"). Let
denote the uniform norm on functions on E. Define the Skorokhod metric σ on D by
where I: E → E is the identity function. In terms of the"wiggle" intuition, ||λ − I|| measures the size of the"wiggle in time", and ||ƒ − g○λ|| measures the size of the"wiggle in space".
It can be shown that the Skorokhod metric is, indeed a metric. The topology Σ generated by σ is called the Skorokhod topology on D.
Properties of Skorokhod space
Generalization of the uniform topology
The space C of continuous functions on E is a subspace of D. The Skorokhod topology relativized to C coincides with the uniform topology there.
Completeness
It can be shown[citation needed] that, although D is not a complete space with respect to the Skorokhod metric σ, there is a topologically equivalent metric σ0 with respect to which D is complete.
Separability
With respect to either σ or σ0, D is a separable space. Thus, Skorokhod space is a Polish space.
Tightness in Skorokhod space
By an application of the Arzelà–Ascoli theorem, one can show that a sequence (μn)n=1,2,… of probability measures on Skorokhod space D is tight if and only if both the following conditions are met:
and
Algebraic and topological structure
Under the Skorokhod topology and pointwise addition of functions, D is not a topological group.[citation needed]
References
Categories:- Real analysis
- Stochastic processes
Wikimedia Foundation. 2010.