- Holomorphic function
-
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain. The existence of a complex derivative is a very strong condition, for it implies that any holomorphic function is actually infinitely differentiable and equal to its own Taylor series.
The term analytic function is often used interchangeably with “holomorphic function”, although the word “analytic” is also used in a broader sense to describe any function (real, complex, or of more general type) that is equal to its Taylor series in a neighborhood of each point in its domain. The fact that the class of complex analytic functions coincides with the class of holomorphic functions is a major theorem in complex analysis.
Holomorphic functions are also sometimes referred to as regular functions[1] or as conformal maps. A holomorphic function whose domain is the whole complex plane is called an entire function. The phrase "holomorphic at a point z0" means not just differentiable at z0, but differentiable everywhere within some neighborhood of z0 in the complex plane.
Contents
Definition
Given a complex-valued function ƒ of a single complex variable, the derivative of ƒ at a point z0 in its domain is defined by the limit
This is the same as the definition of the derivative for real functions, except that all of the quantities are complex. In particular, the limit is taken as the complex number z approaches z0, and must have the same value for any sequence of complex values for z that approach z0 on the complex plane. If the limit exists, we say that ƒ is differentiable at the point z0. This concept of complex differentiability shares several properties with real differentiability: it is linear and obeys the product rule, quotient rule, and chain rule.
If ƒ is complex differentiable at every point z0 in U, we say that ƒ is holomorphic on U. We say that ƒ is holomorphic at the point z0 if it is holomorphic on some neighborhood of z0. We say that ƒ is holomorphic on some non-open set A if it is holomorphic in an open set containing A.
The relationship between real differentiability and complex differentiability is the following. If a complex function ƒ(x + i y) = u(x, y) + i v(x, y) is holomorphic, then u and v have first partial derivatives with respect to x and y, and satisfy the Cauchy–Riemann equations:
If continuity is not a given, the converse is not necessarily true. A simple converse is that if u and v have continuous first partial derivatives and satisfy the Cauchy–Riemann equations, then ƒ is holomorphic. A more satisfying converse, which is much harder to prove, is the Looman–Menchoff theorem: if ƒ is continuous, u and v have first partial derivatives, and they satisfy the Cauchy–Riemann equations, then ƒ is holomorphic.
Terminology
The word "holomorphic" was introduced by two of Cauchy's students, Briot (1817–1882) and Bouquet (1819–1895), and derives from the Greek ὅλος (holos) meaning "entire", and μορφή (morphē) meaning "form" or "appearance".[2]
Today, the term "holomorphic function" is sometimes preferred to "analytic function", as the latter is a more general concept. This is also because an important result in complex analysis is that every holomorphic function is complex analytic, a fact that does not follow directly from the definitions. The term "analytic" is however also in wide use.
Properties
Because complex differentiation is linear and obeys the product, quotient, and chain rules, the sums, products and compositions of holomorphic functions are holomorphic, and the quotient of two holomorphic functions is holomorphic wherever the denominator is not zero.
The derivative f'(a) can be written as a contour integral using Cauchy's differentiation formula:
for any simple loop positively winding once around a, and
for infinitesimal positive loops γ around a.
If one identifies C with R2, then the holomorphic functions coincide with those functions of two real variables with continuous first derivatives which solve the Cauchy-Riemann equations, a set of two partial differential equations.
Every holomorphic function can be separated into its real and imaginary parts, and each of these is a solution of Laplace's equation on R2. In other words, if we express a holomorphic function f(z) as u(x, y) + i v(x, y) both u and v are harmonic functions.
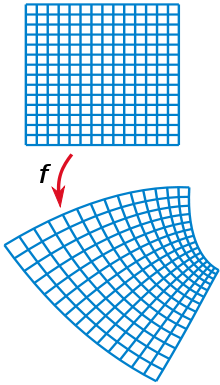
In regions where the first derivative is not zero, holomorphic functions are conformal in the sense that they preserve angles and the shape (but not size) of small figures.
Cauchy's integral formula states that every function holomorphic inside a disk is completely determined by its values on the disk's boundary.
Every holomorphic function is analytic. That is, a holomorphic function f has derivatives of every order at each point a in its domain, and it coincides with its own Taylor series at a in a neighborhood of a. In fact, f coincides with its Taylor series at a in any disk centered at that point and lying within the domain of the function.
From an algebraic point of view, the set of holomorphic functions on an open set is a commutative ring and a complex vector space. In fact, it is a locally convex topological vector space, with the seminorms being the suprema on compact subsets.
From a geometric perspective, a function f is holomorphic at z0 if and only if its exterior derivative df in a neighborhood U of z0 is equal to f′(z) dz for some continuous function f′. It follows from
that df′ is also proportional to dz, implying that the derivative f′ is itself holomorphic and thus that f is infinitely differentiable. Similarly, the fact that d(f dz) = f′ dz ∧ dz = 0 implies that any function f that is holomorphic on the simply connected region U is also integrable on U. (For a path γ from z0 to z lying entirely in U, define
 ;
;
in light of the Jordan curve theorem and the generalized Stokes' theorem, Fγ(z) is independent of the particular choice of path γ, and thus F(z) is a well-defined function on U having F(z0) = F0 and dF = f dz.)
Examples
All polynomial functions in z with complex coefficients are holomorphic on C, and so are sine, cosine and the exponential function. (The trigonometric functions are in fact closely related to and can be defined via the exponential function using Euler's formula). The principal branch of the complex logarithm function is holomorphic on the set C \ {z ∈ R : z ≤ 0}. The square root function can be defined as
and is therefore holomorphic wherever the logarithm log(z) is. The function 1/z is holomorphic on {z : z ≠ 0}.
As a consequence of the Cauchy–Riemann equations, a real-valued holomorphic function must be constant. Therefore, the absolute value of z, the argument of z, the real part of z and the imaginary part of z are not holomorphic. Another typical example of a continuous function which is not holomorphic is complex conjugation.
Several variables
A complex analytic function of several complex variables is defined to be analytic and holomorphic at a point if it is locally expandable (within a polydisk, a Cartesian product of disks, centered at that point) as a convergent power series in the variables. This condition is stronger than the Cauchy–Riemann equations; in fact it can be stated as follows:
A function of several complex variables is holomorphic if and only if it satisfies the Cauchy–Riemann equations and is locally square-integrable.
Extension to functional analysis
Main article: infinite-dimensional holomorphyThe concept of a holomorphic function can be extended to the infinite-dimensional spaces of functional analysis. For instance, the Fréchet or Gâteaux derivative can be used to define a notion of a holomorphic function on a Banach space over the field of complex numbers.
References
- ^ Springer Online Reference Books, Wolfram MathWorld
- ^ Markushevich, A.I.; Silverman, Richard A. (ed.) (2005) [1977]. Theory of functions of a Complex Variable (2nd ed. ed.). New York: American Mathematical Society. p. 112. ISBN 0-8218-3780-X. http://books.google.com/books?id=H8xfPRhTOcEC&dq.
See also
Categories:- Complex analysis
- Functions and mappings
- Types of functions
Wikimedia Foundation. 2010.