- Mesoamerican Long Count calendar
-
"Long Count" redirects here. For the 1927 boxing match, see The Long Count Fight.
 Detail showing three columns of glyphs from a portion of the 2nd century CE La Mojarra Stela 1. The left column gives a Long Count date of 8.5.16.9.7, or 156 CE. The two right columns visible are glyphs from the Epi-Olmec script.
Detail showing three columns of glyphs from a portion of the 2nd century CE La Mojarra Stela 1. The left column gives a Long Count date of 8.5.16.9.7, or 156 CE. The two right columns visible are glyphs from the Epi-Olmec script.
The Mesoamerican Long Count calendar is a non-repeating, vigesimal (base-20) and base-18 calendar used by several Pre-Columbian Mesoamerican cultures, most notably the Maya. For this reason, it is sometimes known as the Maya (or Mayan) Long Count calendar. Using a modified vigesimal tally, the Long Count calendar identifies a day by counting the number of days passed since a mythical creation date that corresponds to August 11, 3114 BCE in the Gregorian calendar.[n 1] The Long Count calendar was widely used on monuments.
Contents
Background
Among other calendars devised in pre-Columbian Mesoamerica, two of the most widely used were the 365-day solar calendar (the Maya version is known as the Haab') and the 260-day calendar, with 20 periods of 13 days. In Mayan studies this 260-day calendar is known as the Tzolk'in; the equivalent Aztec calendar is known by a Nahuatl name, tonalpohualli.
The Haab' and the Tzolk'in calendars identified and named the days, but not the years. The combination of a Haab' date and a Tzolk'in date identifies a specific date in a combination which did not occur again for 52 years. The two calendars based on 365 days and 260 days repeat every 52 Haab' years, a period generally known as the Calendar Round. To designate dates over periods longer than 52 years, some Mesoamericans utilized the Long Count calendar.
Long Count periods
The Long Count calendar identifies a date by counting the number of days from a starting date that is generally calculated to be August 11, 3114 BCE in the proleptic Gregorian calendar or September 6 in the Julian calendar (or −3113 in astronomical year numbering). There has been much debate over the precise correlation between the Western calendars and the Long Count calendars. The August 11 date is based on the GMT correlation (see Correlations between Western calendars and the Long Count calendar section elsewhere in this article for details on correlations).
The completion of 13 b'ak'tuns (August 11, 3114 BCE) marks the Creation of the world of human beings according to the Maya. On this day, Raised-up-Sky-Lord caused three stones to be set by associated gods at Lying-Down-Sky, First-Three-Stone-Place. Because the sky still lay on the primordial sea, it was black. The setting of the three stones centered the cosmos which allowed the sky to be raised, revealing the sun.[1]
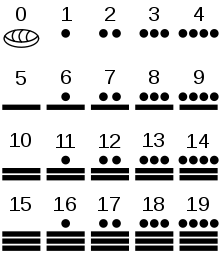
Rather than using a base-10 scheme, like Western numbering, the Long Count days were tallied in a base-20 and base-18 scheme. Thus 0.0.0.1.5 is equal to 25, and 0.0.0.2.0 is equal to 40. The Long Count is not consistently base-20, however, since the second digit from the right rolls over to zero when it reaches 18. Thus 0.0.1.0.0 does not represent 400 days, but rather only 360 days.
The following table shows the period equivalents as well as Maya names for these periods:
Representation Long Count subdivisions Days ~ solar years 0.0.0.0.1 1 k'in 1 1/365 0.0.0.1.0 1 winal = 20 k'in 20 0.055 0.0.1.0.0 1 tun = 18 winal 360 0.986 0.1.0.0.0 1 k'atun = 20 tun 7,200 19.71 1.0.0.0.0 1 b'ak'tun = 20 k'atun 144,000 394.3 Note that the name b'ak'tun is a back-formation invented by scholars. The numbered Long Count was no longer in use by the time the Spanish arrived in the Yucatán Peninsula, although unnumbered k'atuns and tuns were still in use.[citation needed]
Calculating Long Count dates
Mesoamerican numerals
 The back of Stela C from Tres Zapotes, an Olmec archaeological site.
The back of Stela C from Tres Zapotes, an Olmec archaeological site.
This is the second oldest Long Count date yet discovered. The numerals 7.16.6.16.18 translate to September 1, 32 BCE (Gregorian). The glyphs surrounding the date are what is thought to be one of the few surviving examples of Epi-Olmec script.See also: History of zero.Long Count dates are written with Mesoamerican numerals, as shown on this table. A dot represents 1 while a bar equals 5. The shell glyph was used to represent the zero concept. The Long Count calendar required the use of zero as a place-holder, and presents one of the earliest uses of the zero concept in history.
Numerical order
The Long Count dates are written vertically, with the higher periods (i.e. b'ak'tun) on the top and then the number of each successively smaller order periods until the number of days (k'in) are listed. As can be seen at left, the Long Count date shown on Stela C at Tres Zapotes is 7.16.6.16.18.
7 × 144000 = 1,008,000 days (k'in) 16 × 7200 = 115,200 days (k'in) 6 × 360 = 2,160 days (k'in) 16 × 20 = 320 days (k'in) 18 × 1 = 18 days (k'in) Total days = 1,125,698 days (k'in) The date on Stela C, then, is 1,125,698 days from August 11, 3114 BCE, Julian day number 1,709,981, September 1, 32 BCE in the proleptic Gregorian calendar, September 3, −31 in the Julian calendar with astronomical year numbering.
On Maya monuments, the Long Count syntax is more complex. The date sequence is given once, at the beginning of the inscription, and opens with the so-called ISIG (Introductory Series Initial Glyph) which reads tzik-a(h) hab’ [patron of Haab' month] ("revered was the year-count with the patron [of the month]").[2] Next come the 5 digits of the Long Count, followed by the Calendar Round (tzolk'in and Haab') and supplementary series series. The supplementary series is optional and contains lunar data, for example, the age of the moon on the day and the calculated length of current lunation.[n 2] The text then continues with whatever activity occurred on that date.
A drawing of a full Maya Long Count inscription is shown below.
Earliest Long Counts
The earliest Long Count inscription yet discovered is on Stela 2 at Chiapa de Corzo, Chiapas, Mexico, showing a date of 36 BCE.[n 3] This table lists the six artifacts with the eight oldest Long Counts according to Vincent H. Malmström.[3]
Archaeological site Name Gregorian date GMT (584283) correlation
Long Count Location Chiapa de Corzo Stela 2 December 6, 36 BCE 7.16.3.2.13 Chiapas, Mexico Tres Zapotes Stela C September 1, 32 BCE 7.16.6.16.18 Veracruz, Mexico El Baúl Stela 1 March 2, 37 CE 7.19.15.7.12 Guatemala Abaj Takalik Stela 5 May 19, 103 CE 8.3.2.10.15 " " " June 3, 126 CE 8.4.5.17.11 " La Mojarra Stela 1 May 19, 143 CE 8.5.3.3.5 Veracruz, Mexico " " July 11, 156 CE 8.5.16.9.7 " Near La Mojarra Tuxtla Statuette March 12, 162 CE 8.6.2.4.17 " Of the six sites, three are on the western edge of the Maya homeland and three are several hundred kilometers further west, leading most researchers to believe that the Long Count calendar predates the Maya.[4] La Mojarra Stela 1, the Tuxtla Statuette, Tres Zapotes Stela C, and Chiapa Stela 2 are all inscribed in an Epi-Olmec, not Maya, style.[5] El Baúl Stela 2, on the other hand, was created in the Izapan style. The first unequivocally Maya artifact is Stela 29 from Tikal, with the Long Count date of 292 CE (8.12.14.8.15), more than 300 years after Stela 2 from Chiapa de Corzo.[6]
Correlations between Western calendars and the Long Count
The Maya and western calendars are correlated by using a Julian day number of the starting date of the current creation – 13.0.0.0.0 4 Ajaw, 8 Kumk'u.[n 4] This is referred to as a correlation constant. The generally accepted correlation constant is the Modified Thompson 2, "Goodman, Martinez, Thompson" – GMT correlation of 584,283 days. Using the GMT correlation the current creation started on September 6, 3114 BC (Julian) or August 11 in the Proleptic Gregorian calendar. The study of correlating the Maya and western calendar is referred to as the correlation question.[7][8][9][10][11] In Breaking the Maya Code, Michael Coe writes: "In spite of oceans of ink that have been spilled on the subject, there now is not the slightest chance that these three scholars (conflated to GMT when talking about the correlation) were not right...".[12]
The evidence for the GMT correlation is historical, astronomical, and archaeological:
Historical: Calendar Round dates with a corresponding Julian date are recorded in Diego de Landa's Relación de las cosas de Yucatán, the Chronicle of Oxcutzkab and the books of Chilam Balam. Oxcutzkab and de Landa record a date that is a Tun ending. Regarding these historical references in The Skywatchers Aveni writes: "All the assembled data are consistent with the equation November 3, 1539 = 11.16.0.0.0. Thus for the GMT, or 11.16 correlation we find that A = 584,283...".[13] The fall of the capital city of the Aztec Empire, Tenochtitlan, occurred on August 13, 1521. A number of different chroniclers wrote that this was a Tzolk'in (Tonalpohualli) of 1 Snake. Post-conquest scholars such as Sahagun and Duran recorded Aztec calendar dates with a calendar date. Many indigenous Guatemalan communities, principally those speaking the Mayan languages known as Ixil, Mam, Pokomchí, and Quiché, keep the Tzolk'in and (in many cases) the Haab'[14] and in Veracruz, Oaxaca and Chiapas, Mexico[15] These are all consistent with the GMT correlation.
Astronomical: Any correct correlation must match the astronomical content of classic inscriptions. The GMT correlation does an excellent job of matching lunar data in the supplementary series.[16] For example: An inscription at the Temple of the Sun at Palenque records that on Long Count 9.16.4.10.8 there were 26 days completed in a 30 day lunation.[n 5] The Dresden Codex contains an eclipse table[22] which gives eclipse seasons when the Moon is near its ascending or descending node and an eclipse is likely to occur. Dates converted using the GMT correlation fall roughly in this eclipse season. The Dresden Codex contains a Venus table which records the heliacal risings of Venus. The GMT correlation agrees with these to within a few days which is as accurately as these could have been observed by the ancient Maya.
Archaeological: Various items that can be associated with specific Long Count dates have been isotope dated. In 1959 the University of Pennsylvania carbon dated samples from ten wood lintels from Tikal.[23] These were carved with a date equivalent to 741 AD using the GMT correlation. The average carbon date was 746±34 years.
If a proposed correlation only has to agree with one of these lines of evidence there could be numerous other possibilities. Astronomers have proposed many correlations, for example: Lounsbury,[24] Fuls, et. al.,[25] Böhm and Böhm[26] and Stock.[27]
Today, 02:13, Tuesday November 22, 2011 (UTC), in the Long Count is 12.19.18.16.5 (GMT correlation).
JDN correlations
to the Maya creation date
(after Thompson 1971, et al. and Aveni 1980)Name Correlation Bowditch 394,483 Willson 438,906 Smiley 482,699 Makemson 489,138 Modified Spinden 489,383 Spinden 489,384 Teeple 492,622 Dinsmoor 497,879 −4CR 508,363 −2CR 546,323 Stock 556,408 Goodman 584,280 Martinez-Hernandez 584,281 GMT 584,283 Modified Thompson 1 584,284 Thompson (Lounsbury) 584,285 Pogo 588,626 +2CR 622,243 Böhm 622,261 Kreichgauer 626,927 +4CR 660,203 Fuls, et. al. 660,208 Hochleitner 674,265 Schultz 677,723 Escalona-Ramos 679,108 Valliant 679,183 Weitzel 774,078 Long Count[n 6] Gregorian date
GMT (584283) correlation13.0.0.0.0 August 11, 3114 BCE 1.0.0.0.0 November 13, 2720 BCE 2.0.0.0.0 February 16, 2325 BCE 3.0.0.0.0 May 21, 1931 BCE 4.0.0.0.0 August 23, 1537 BCE 5.0.0.0.0 November 26, 1143 BCE 6.0.0.0.0 February 28, 748 BCE 7.0.0.0.0 June 3, 354 BCE 8.0.0.0.0 September 5, 41 CE 9.0.0.0.0 December 9, 435 10.0.0.0.0 March 13, 830 11.0.0.0.0 June 15, 1224 12.0.0.0.0 September 18, 1618 13.0.0.0.0 December 21, 2012 14.0.0.0.0 March 26, 2407 15.0.0.0.0 June 28, 2801 16.0.0.0.0 October 1, 3195 17.0.0.0.0 January 3, 3590 18.0.0.0.0 April 7, 3984 19.0.0.0.0 July 11, 4378 1.0.0.0.0.0 October 13, 4772 2012 and the Long Count
Main article: 2012 phenomenonAccording to the Popol Vuh, a book compiling details of creation accounts known to the K'iche' Maya of the Colonial-era highlands, we are living in the fourth world.[29] The Popol Vuh describes the first three creations that the gods failed in making and the creation of the successful fourth world where men were placed. In the Maya Long Count, the previous creation ended at the start of a 14th b'ak'tun.
The previous creation ended on a long count of 12.19.19.17.19. Another 12.19.19.17.19 will occur on December 20, 2012, followed by the start of the 14th b'ak'tun, 13.0.0.0.0, on December 21, 2012.[n 7] There is only one reference to the current creation's 13th b'ak'tun in the fragmentary Mayan corpus: Tortuguero Monument 6, part of a ruler's inscription.
Maya inscriptions occasionally reference future predicted events or commemorations that would occur on dates that lie beyond 2012 (that is, beyond the completion of the 13th b'ak'tun of the current era). Most of these are in the form of "distance dates" where some Long Count date is given, together with a Distance Number that is to be added to the Long Count date to arrive at this future date.
For example, on the west panel at the Temple of Inscriptions in Palenque, a section of the text projects into the future to the 80th Calendar Round (CR) 'anniversary' of the famous Palenque ruler K'inich Janaab' Pakal's accession to the throne (Pakal's accession occurred on a Calendar Round date 5 Lamat 1 Mol, at Long Count 9.9.2.4.8 equivalent to 27 July 615 CE in the proleptic Gregorian calendar).[n 8] It does this by commencing with Pakal's birthdate 9.8.9.13.0 8 Ajaw 13 Pop (24 March 603 CE Gregorian) and adding to it the Distance Number 10.11.10.5.8.[31] This calculation arrives at the 80th Calendar Round since his accession, a day that also has a CR date of 5 Lamat 1 Mol, but which lies over 4,000 years in the future from Pakal's time—the day 21 October in the year 4772. The inscription notes[citation needed] that this day would fall eight days after the completion of the 1st piktun [since the creation or zero date of the Long Count system], where the piktun is the next-highest order above the b'ak'tun in the Long Count. If the completion date of that piktun—13 October 4772—were to be written out in Long Count notation, it could be represented as 1.0.0.0.0.0. The 80th CR anniversary date, eight days later, would be 1.0.0.0.0.8 5 Lamat 1 Mol.[31][32]
Despite the publicity generated by the 2012 date, Susan Milbrath, curator of Latin American Art and Archaeology at the Florida Museum of Natural History, stated that "We have no record or knowledge that [the Maya] would think the world would come to an end" in 2012.[33] "For the ancient Maya, it was a huge celebration to make it to the end of a whole cycle," says Sandra Noble, executive director of the Foundation for the Advancement of Mesoamerican Studies in Crystal River, Florida. To render December 21, 2012, as a doomsday event or moment of cosmic shifting, she says, is "a complete fabrication and a chance for a lot of people to cash in."[33] "There will be another cycle," says E. Wyllys Andrews V, director of the Tulane University Middle American Research Institute (MARI). "We know the Maya thought there was one before this, and that implies they were comfortable with the idea of another one after this."[34]
Calculating a full Long Count date
 Chichen Itza Initial Series inscription. This date (glyphs A2, B2, …, A5) is 10.2.9.1.9 9 Muluk 7 Sak, equivalent to July 28, 878 (GMT Gregorian).
Chichen Itza Initial Series inscription. This date (glyphs A2, B2, …, A5) is 10.2.9.1.9 9 Muluk 7 Sak, equivalent to July 28, 878 (GMT Gregorian).
As stated, a full Long Count date not only includes the five digits of the Long Count, but the 2-character Tzolk'in and the two-character Haab' dates as well. The five digit Long Count can therefore be confirmed with the other four characters (the "calendar round date").
Taking as an example a Calendar Round date of 9.12.2.0.16 (Long Count) 5 Kib' (Tzolk'in) 14 Yaxk'in (Haab'). One can check whether this date is correct by the following calculation.
It is perhaps easier to find out how many days there are since 4 Ajaw 8 Kumk'u, and show how the date 5 Kib' 14 Yaxk'in is derived.
9 × 144000 = 1296000 12 × 7200 = 86400 2 × 360 = 720 0 × 20 = 0 16 × 1 = 16 Total days = 1383136 Calculating the Tzolk'in date portion
The Tzolk'in date is counted forward from 4 Ajaw. To calculate the numerical portion of the Tzolk'in date, we must add 4 to the total number of days given by the date, and then divide total number of days by 13.
- (4 + 1383136) / 13 = 106395 and 5/13
This means that 106395 whole 13 day cycles have been completed, and the numerical portion of the Tzolk'in date is 5.
To calculate the day, we divide the total number of days in the long count by 20 since there are twenty day names.
- 1383136 / 20 = 69156 and (16/20)
This means 16 day names must be counted from Ajaw. This gives Kib'. Therefore, the Tzolk'in date is 5 Kib'.
Calculating the Haab' date portion
The Haab' date 8 Kumk'u is the ninth day of the eighteenth month. Since there are twenty days per month, there are eleven days remaining in Kumk'u. The nineteenth and last month of the Haab' year contains only five days, thus, there are sixteen days until the end of the Haab' year.
If we subtract 16 days from the total, we can then find how many complete Haab' years are contained.
- 1383136 − 16 = 1383120
Dividing by 365, we have
- 1383120 / 365 = 3789 and (135/365)
Therefore, 3789 complete Haab' have passed, with 135 days into the new Haab'.
We then find which month the day is in. Dividing the remainder 135 days by 20, we have six complete months, plus 15 remainder days. So, the date in the Haab' lies in the seventh month, which is Yaxk'in. The fifteenth day of Yaxk'in is 14, thus the Haab' date is 14 Yaxk'in.
So the date of the long count date 9.12.2.0.16 5 Kib' 14 Yaxk'in is confirmed.
Piktuns and higher orders
As mentioned in the Syntax section, there are also four rarely used higher-order periods above the b'ak'tun: piktun, kalabtun, k'inchiltun, and alautun. All of these words are inventions of Mayanists.
The inscription on Quirigua stela F, or 6, shows a Long Count date of 9.16.10.0.0 1 Ahau 3 Zip (March 15, 761 Gregorian). The huge distance date of 1.8.13.0.9.16.10.0.0 is subtracted and the resulting date is given as (18.)13.0.0.0.0.0.0.0 1 Ahau 13 Yaxkin, which is equivalent to a day over 90 million years in the past. However, there is another distance date on Quirigua Stela D or 4, that gives a date of 9.16.15.0.0 7 Ahau 18 Pop (February 17, 766 Gregorian), to which is added 6.8.13.0.9.16.15.0.0, to give a date of (13.)13.0.0.0.0.0.0.0. This is over 400 million years after the date the stela was erected.
The Dresden codex contains another method for linking Long Counts in the prior era to this one. These are not explicitly stated as Long Counts but are implied by a Ring Number – a distance number with the K'in coefficient enclosed in a red loop tied at the top. These are referred to as "Long Reckonings". Long Reckonings are distance numbers which are based on a date in the preceding creation to give a date in the current one. Thompson uses the last example from the Dresden codex:
Ring number (12) 12.12.17.3.1 13 Imix 9 Wo (7.2.14.19 before (13) 13.0.0.0.0)
distance number (0) 10.13.13.3.2
Long Count 10.6.10.6.3 13 Ak'bal 1 Kank'in
A series of "Serpent Numbers" in the Dresden codex pp.61–69 has Long Reckonings from a date 34,000 years in the past to classical Maya Long Counts.By studying these distance dates and Long Reckonings Eric Thompson determined that the date of creation in 3114 BCE – 13.0.0.0.0 was actually ...13.13.0.0.0.0 in the extended version.
At Yaxchilan, on a temple stairway, there is an inscription that includes four levels above the alautuns. The inscription reads: 13.13.13.13.13.13.13.13.9.15.13.6.9 3 Muluc 17 Mac. This is equivalent to October 19, 744, but the higher cycles do not conform to Thompson’s calculation. The same applies to a Late Classic monument from Coba, Stela 1. The date of creation is expressed as 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, where the units are 13s in the nineteen places larger than the b'ak'tun.[35][36]
See also
Notes
- ^ The correlation between the Long Count and Western calendars is calculated according to the one used by a majority of Maya researchers, known as the (modified) GMT or Goodman-Martinez-Thompson correlation. An alternate correlation sometimes used puts the starting date two days later. August 11, 3114 BCE is a date in the proleptic Gregorian calendar, which equates to September 6, 3114 BCE in the Julian calendar and −3113 in astronomical year numbering. See Correlations between Western calendars and the Long Count calendar section elsewhere in this article for details on correlations.
- ^ Notable in this sequence is the glyph with nine variant forms labeled G by early epigraphers. It has been connected with the cycle of Lords of the Night known from colonial era sources in Central Mexico but alternate explanations have also been offered. See Thompson.
- ^ To clarify, there are Long Count inscriptions which refer to dates earlier than 36 BCE, but these were carved much later than those dates.
- ^ All extant Maya inscriptions that represent this base date wrote it with a 13 Bak'tuns, not 0, however, when using this as a base date in calculations this 13 functions mathematically as if it were a zero.
- ^ Modern astronomers refer to the conjunction of the Sun and Moon (the time when the Sun and Moon have the same ecliptic longitude) as the new moon. For the Maya, new moon was the first evening when one could look to the west after sunset and see the thin crescent moon. Given our modern ability to know exactly where to look, when the crescent Moon is favorably located, from an excellent site, on rare occasions observers can see and photograph the crescent moon less than one day after conjunction. Generally, most observers won't see the new Moon until the first evening when the lunar phase day is at least 1.5.[17][18][19][20][21] If one assumes that that the new moon is the first day when the lunar phase day is at least 1.5 at six in the evening in time zone UTC−6 (the time zone of the Maya area) the GMT correlation will match many lunar inscriptions exactly. In this example the lunar phase day was 27.7 (26 days counting from zero) at 6 pm after a conjunction at 1:25 am October 10, 755 and a new Moon when the lunar phase day was 1.7 at 6 pm on October 11, 755 (Julian calendar).
- ^ Freidel, Schele & Parker use 13 for higher order positions of piktuns and kalatuns (for example, 13.13.13.0.0.0.0) when not occupied by 1 or 0 to conform to the unlimited number of 13s larger than b'ak'tuns discussed in Piktuns and higher orders. B'ak'tuns 2–12 & 14–19 are interpolated between the authors' 13.13.1.0.0.0.0, 13.13.13.0.0.0.0 and 13.1.0.0.0.0.0.[28]
- ^ Various sources place this on other dates, notably on December 23.[30]
- ^ Gregorian, using GMT correlation JDN=584283.
References
- ^ Freidel, Schele & Parker (1993, pp.59–75).
- ^ Boot, p. 2.
- ^ Vincent H. Malmström, Cycles of the Sun, Mysteries of the Moon (Chapter 6) Malmström's Gregorian dates are three or four days later than a correlation of 584283 would give (the Wikipedia table has been corrected).
- ^ Diehl (2004, p.186).
- ^ "A sketch of prior documentation of epi-Olmec texts", Section 5 in Peréz de Lara & Justeson (2005).
- ^ Coe & Koontz (2002, p.87)
- ^ Maya chronology: The correlation question by J. Eric Thompson
- ^ Maya Hieroglyphic Writing by Sir John Eric Sidney Thompson
- ^ Clarifications: The Correlation Debate
- ^ The Correlation Problem
- ^ What is this correlation constant?
- ^ Breaking the Maya Code, 1992, p. 114.
- ^ Anthony F. Aveni, The Sky Watchers, 201, pp. 208–210.
- ^ Barbara Tedlock, Time and the Highland Maya Revised edition (1992 Page 1)
- ^ Miles, Susanna W, "An Analysis of the Modern Middle American Calendars: A Study in Conservation." In Acculturation in the Americas. Edited by Sol Tax, pp. 273–84. Chicago: University of Chicago Press, 1952.
- ^ The Supplementary and Lunar Glyphs
- ^ "Sighting the Crescent Moon", Sky & Telescope, July 1994, 14
- ^ "In Quest of the Youngest Moon", Sky & Telescope, December 1996, 104–105
- ^ "Young Moons and the Islamic Calendar", Sky & Telescope, December 1996, 106
- ^ "Seeking Thin Crescent Moons", Sky & Telescope, February 2004, 102–106
- ^ "Young-Moon Hunting in 2005", Sky and Telescope, February 2005, 75–76
- ^ The Dresden Codex eclipse table by Michael John Finley
- ^ "Review of radiocarbon dates from Tikal and the Maya calendar correlation problem" by Elizabeth K. Ralph
- ^ Academic Confusion by John Major Jenkins
- ^ The Correlation Question by Andreas Fuls
- ^ Mayan Dating by Vladimir Böhm and Bohumil Böhm
- ^ Dating the Eclipse Table of the Dresden Codex and the Correlation Problem
- ^ Freidel, Schele & Parker (1993, p. 63)
- ^ Schele & Freidel (1990, pp.429–430
- ^ Schele and Friedel (1992).
- ^ a b Schele (1992, pp.93–95)
- ^ Schele & Freidel (1990, p.430 n.39)
- ^ a b Susan Milbrath, Curator of Latin American Art and Archaeology, Florida Museum of Natural History, quoted in USA Today, Wednesday, March 28, 2007, p. 11D
- ^ "The Sky Is Not Falling" New Wave, Tulane University, June 25, 2008.
- ^ Fig. 444 in Wagner (2006, p.283)
- ^ Schele and Freidel (1992, p.430).
Bibliography
-
- Boot, Eric (2002). "The Dos Pilas-Tikal Wars from the Perspective of Dos Pilas Hieroglyphic Stairway 4" (PDF). Mesoweb Articles. Mesoweb. http://www.mesoweb.com/features/boot/DPLHS4.pdf. Retrieved 2007-03-15.
- Coe, Michael D. (1992). Breaking the Maya Code. London and New York: Thames & Hudson. ISBN 0-500-05061-9. OCLC 26605966.
- Coe, Michael D.; with Rex Koontz (2002). Mexico: from the Olmecs to the Aztecs (5th, revised and enlarged ed.). London and New York: Thames & Hudson. ISBN 0-500-28346-X. OCLC 50131575.
- Coe, Michael D.; and Mark L Van Stone (2005). Reading the Maya Glyphs. London: Thames & Hudson. ISBN 9780500285534.
- Diehl, Richard (2004). The Olmecs: America's First Civilization. Ancient peoples and places series. London: Thames & Hudson. ISBN 0-500-02119-8. OCLC 56746987.
- Freidel, David; and Linda Schele and Joy Parker (1993). Maya Cosmos: Three thousand years on the shaman's path. New York: William Morrow. ISBN 0-888-10081-5. OCLC 27430287.
- Gronemeyer, Sven (2006). "Glyphs G and F: Identified as Aspects of the Maize God" (PDF). Wayeb Notes 22: pp.1–23. ISSN 1379-8286. http://www.wayeb.org/notes/wayeb_notes0022.pdf. Retrieved 2007-04-04.
- Kelley, David H. (2005). Exploring Ancient Skies: an Encyclopedic Survey of Archaeoastronomy. Berlin: Springer Verlag. ISBN 0387953108.
- Kelley, David H. (2008). "Archaeoastronomy". In Deborah M. Pearsall. Encyclopedia of Archaeology, Vol. 1: A. Oxford: Academic Press. pp. 451–464. ISBN 978-0-12-548030-7. OCLC 2007931569.
- MacDonald, G. Jeffrey (27 March 2007). "Does Maya calendar predict 2012 apocalypse?" (online edition). USA Today (McLean, VA: Gannett Company): p. 11D. ISSN 0734-7456. http://www.usatoday.com/tech/science/2007-03-27-maya-2012_n.htm. Retrieved 2009-05-28.
- Pérez de Lara, Jorge; and John Justeson (2005). "Photographic Documentation of Monuments with Epi-Olmec Script/Imagery". The Foundation Granting Department: Reports Submitted to FAMSI. Foundation for the Advancement of Mesoamerican Studies, Inc. (FAMSI). http://www.famsi.org/reports/05084/index.html. Retrieved 2007-04-04.
- Schele, Linda (1992). "A New Look at the Dynastic History of Palenque". In Victoria R. Bricker (Volume ed.), with Patricia A. Andrews. Supplement to the Handbook of Middle American Indians, Vol. 5: Epigraphy. Victoria Reifler Bricker (general editor). Austin: University of Texas Press. pp. 82–109. ISBN 0-292-77650-0. OCLC 23693597.
- Schele, Linda; and David Freidel (1990). A Forest of Kings: The Untold Story of the Ancient Maya (pbk reprint of 1990 ed.). New York: Harper Perennial. ISBN 0-688-11204-8. OCLC 145324300.
- Thompson, J. Eric S. (1929). "Maya Chronology: Glyph G of the Lunar Series". American Anthropologist, New Series 31 (2): pp.223–231. doi:10.1525/aa.1929.31.2.02a00010. ISSN 0002-7294. OCLC 51205515.
- Thompson, J. Eric S. (1971). Maya Hieroglyphic Writing, an Introduction. 3rd edition. Norman.
- ISBN 978-0982682609.
- Voss, Alexander W.; and H. Juergen Kremer (2000). "K'ak'-u-pakal, Hun-pik-tok' and the Kokom:The Political Organisation of Chichen Itza" (PDF). 3rd European Maya Conference (1998). http://ecoyuc.com.mx/articles.php?task=detail&aid=1. Retrieved 2005-10-26.
- Wagner, Elizabeth (2006). "Maya Creation Myths and Cosmology". In Nikolai Grube (ed.). Maya: Divine Kings of the Rain Forest. Eva Eggebrecht and Matthias Seidel (assistant eds.). Cologne: Könemann. pp. 280–293. ISBN 3-8331-1957-8. OCLC 71165439.
External links
- Today's date according to the Long Count, in pictorial form.
- Today's date according to the Long Count, in form of a miles count.
- Coba Stela 1 (Schele #4087), partial illustration from the Linda Schele Drawings Collection of the monument from Coba with an expanded Long Count date
- The Maya Calendar by the Maya World Studies Center in Yucatán Mexico
- Maya calendar on michielb.nl, with conversion applet from Gregorian calendar to Maya date (Uses the proleptic Gregorian calendar.)
- UT Mesoamerica Center Discussion Board. (David Stuart's translation of Monument 6 at Tortuguero.)
- Maya Calendar and Links on diagnosis2012.co.uk (The calculator uses the proleptic Gregorian calendar. The site has a huge number of links to Maya calendar sites.)
- Culture and History of the Ancient and Modern Maya Includes pdf files of "Popol Vuh: The Book of the Counsil" and "Chilam Balam of Chumayel" (The page about the calendar uses the "astronomical" (Lounsbury) correlation.)
- The Dresden Codex Lunar Series and Sidereal Astronomy
- Day Symbols of the Maya Year at Project Gutenberg 1897 text by Cyrus Thomas.
Calendars (list) Wide use Selected use Akan · Armenian · Assyrian · Aztec (Tonalpohualli · Xiuhpohualli) · Babylonian · Bahá'í · Bengali · Berber · Bikram Samwat · Buddhist · Bulgar · Burmese · Byzantine · Celtic · Coptic Ethiopian · Hebrew · Hellenic · Hindu (Indian · Malayalam · Tamil) · Igbo · Inca · Iranian (Zoroastrian, Medieval (Jalali), Modern (Hijri)) · Irish · Japanese · Javanese · Juche · Korean · Kurdish · Lithuanian · Maya (Haab' · Tzolk'in) · Minguo · Mongolian · Nanakshahi · Nepal Sambat · Pawukon · Pentecontad · Rapa Nui · Thai (Lunar · Solar) · Tibetan · Vietnamese · Xhosa · Yoruba
Calendar types: Runic · Mesoamerican (Long Count · Calendar round)
Christian variants: Calendar of saints · Eastern Orthodox liturgical calendar · Liturgical year · Revised Julian calendarRarely used Historical Martian Alternative New Age Displays and
applicationsProposed calendars The World Calendar · 13-month calendarYear numbering Fictional Categories:- Mesoamerican calendars
- Specific calendars
- Chronology
- Obsolete calendars
- 2012 phenomenon
Wikimedia Foundation. 2010.